题目内容
2.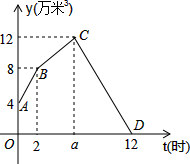 某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.若这3个水口的水流都是匀速的,水池中的蓄水量y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题:
某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.若这3个水口的水流都是匀速的,水池中的蓄水量y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题:(1)蓄水池中原有蓄水4万米3,蓄水池达最大蓄水量12万米3的时间a的值为6;
(2)求线段BC、CD所表示的y与t之间的函数关系式;
(3)蓄水池中蓄水量维持在m万米3以上(含m万米3)的时间有3小时,求m的值.
分析 (1)根据函数图象可以得到蓄水池中原有蓄水的体积,由2个流量相同的进水口和图象可以求得a的值;
(2)根据函数图象可以分别求得线段BC、CD所表示的y与t之间的函数关系式;
(3)由题意可知,BC上的函数值和CD上的函数值相等,且分别对应的时间差值为3,从而可以求得m的值.
解答 解:(1)由图象可知,蓄水池中原有蓄水4万米3,蓄水池达最大蓄水量12万米3的时间a的值为:2+(12-8)÷($\frac{8-4}{2}×\frac{1}{2}$)=6,
故答案为:4,6;
(2)∵B(2,8),C(6,12),设直线BC的函数关系式为y=k1t+b1,
由题意,得$\left\{\begin{array}{l}2{k_1}+{b_1}=8\\ 6{k_1}+{b_1}=12\end{array}\right.$
解得:$\left\{\begin{array}{l}{k_1}=1\\{b_1}=6\end{array}\right.$
即直线BC所对应的函数关系式为y=t+6(2≤t≤6),
∵C(6,12),D(12,0),设直线CD的函数关系式为y=k2t+b2,
由题意,得$\left\{\begin{array}{l}6{k_2}+{b_2}=12\\ 12{k_2}+{b_2}=0\end{array}\right.$
解得:$\left\{\begin{array}{l}{k_2}=-2\\{b_2}=24\end{array}\right.$
即直线CD所对应的函数关系式为y=-2t+24(6≤t≤12);
(3)设在BC上蓄水量达到m万米3的时间为t,则在CD上蓄水量达到m万米3的时间为(t+3)h,
由题意,得t+6=-2(t+3)+24,
解得:t=4,
∴当 t=4时,y=4+6=10
即m的值是10.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

| A. | 要消去y,可以将①×5+②×2 | B. | 要消去x,可以将①×3+②×(-5) | ||
| C. | 要消去y,可以将①×5+②×3 | D. | 要消去x,可以将①×(-5)+②×2 |
| A. | 4 | B. | ±$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
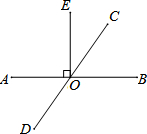 如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.
如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数.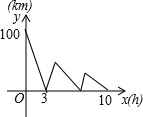 甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.
甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.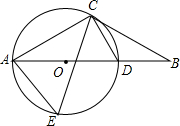 如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.
如图,在△ABC中,AC=BC,∠CAB=30°,过点C作CD⊥AC交AB于点D,⊙O是△ACD的外接圆.