Question

16．芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁，大桥采用低塔斜拉桥桥型（如甲图），图乙是从图甲引申出的平面图，假设你站在桥上测得拉索AB与水平桥面的夹角是30°，拉索CD与水平桥面的夹角是60°，两拉索顶端的距离BC为2米，两拉索底端距离AD为20米，请求出立柱BH的长．（结果精确到0.1米，$\sqrt{3}$≈1.732）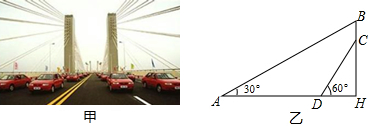

Answer 1

分析 设DH=x米，由三角函数得出=$\sqrt{3}$x，得出BH=BC+CH=2+$\sqrt{3}$x，求出AH=$\sqrt{3}$BH=2$\sqrt{3}$+3x，由AH=AD+DH得出方程，解方程求出x，即可得出结果．

解答 解：设DH=x米，
∵∠CDH=60°，∠H=90°，
∴CH=DH•tan60°=$\sqrt{3}$x，
∴BH=BC+CH=2+$\sqrt{3}$x，
∵∠A=30°，
∴AH=$\sqrt{3}$BH=2$\sqrt{3}$+3x，
∵AH=AD+DH，
∴2$\sqrt{3}$+3x=20+x，
解得：x=10-$\sqrt{3}$，
∴BH=2+$\sqrt{3}$（10-$\sqrt{3}$）=10$\sqrt{3}$-1≈16.3（米）．
答：立柱BH的长约为16.3米．

点评 本题考查了解直角三角形的应用；由三角函数求出CH和AH是解决问题的关键．