题目内容
4. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形
②△AED≌△GED
③∠DFG=112.5°
④BC+FG=1.5
其中正确的结论是①②③.
分析 首先证明△ADE≌△GDE,再求出∠AEF、∠AFE、∠GEF、∠GFE的度数,推出AE=EG=FG=AF,由此可以一一判断.
解答  证明:∵四边形ABCD是正方形,
证明:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DHG是由△DBC旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在Rt△ADE和Rt△GDE中,
$\left\{\begin{array}{l}{DE=DE}\\{DA=DG}\end{array}\right.$,
∴AED≌△GED,故②正确,
∴∠ADE=∠EDG=22.5°,AE=EG,
∴∠AED=∠AFE=67.5°,
∴AE=AF,同理△AEF≌△GEF,可得EG=GF,
∴AE=EG=GF=FA,
∴四边形AEGF是菱形,故①正确,
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°,故③正确.
∵AE=FG=EG=BG,BE=$\sqrt{2}$AE,
∴BE>AE,
∴AE<$\frac{1}{2}$,
∴CB+FG<1.5,故④错误.
故答案为①②③.
点评 本题考查正方形的性质、全等三角形的判定和性质、菱形的判定和性质、等腰直角三角形的性质等知识,解题的关键是通过计算发现角相等,学会这种证明角相等的方法,属于中考常考题型.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
14.下列计算结果正确的是( )
| A. | 8x6÷2x3=4x2 | B. | x2+x3=x5 | C. | (-3x2y)3=-9x6y3 | D. | x•x2=x3 |
15.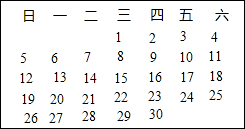 在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )
在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )
 在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )
在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )| A. | 27 | B. | 51 | C. | 69 | D. | 72 |
12. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{3}$ |
8. 如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
 如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )| A. | AB=AE | B. | AB=BE | C. | AE=BE | D. | AB=AC |
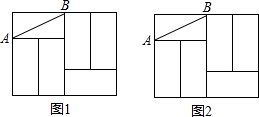 如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$.
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$.