题目内容
1.已知一次函数y=kx+2k+3的图象与y轴的交点在y轴的正半轴上,且函数值y随x的增大而减小,则k所有可能取得的整数值为-1.分析 由一次函数图象与系数的关系可得出关于k的一元一次不等式组,解不等式组即可得出结论.
解答 解:由已知得:$\left\{\begin{array}{l}{2k+3>0}\\{k<0}\end{array}\right.$,
解得:-$\frac{3}{2}$<k<0.
∵k为整数,
∴k=-1.
故答案为:-1.
点评 本题考查了一次函数图象与系数的关系,解题的关键是得出关于k的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据一次函数图象与系数的关系找出关于系数的不等式(或不等式组)是关键.

练习册系列答案
相关题目
12. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{3}$ |
10.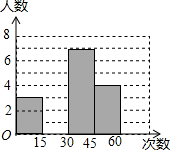 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
(1)频数分布表中a=0.3,b=4,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?
 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:| 分 组 | 频数 | 频率 |
| 第一组(0≤x<15) | 3 | 0.15 |
| 第二组(15≤x<30) | 6 | a |
| 第三组(30≤x<45) | 7 | 0.35 |
| 第四组(45≤x<60) | b | 0.20 |
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?
 如图,已知∠CAB=∠DBA,∠CBD=∠DAC.
如图,已知∠CAB=∠DBA,∠CBD=∠DAC.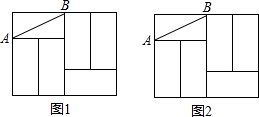 如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
 在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).
在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3). 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$.
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$. 对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如,下图中的函数有0,1两个不变值,其不变长度q等于1.
对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如,下图中的函数有0,1两个不变值,其不变长度q等于1.