题目内容
已知关于x的分式方程
-1=
,求:
(1)若这个方程的解为非负数,求k的取值范围;
(2)若这个方程有增根,求k的值.
| x |
| x-3 |
| k |
| x2-4x+3 |
(1)若这个方程的解为非负数,求k的取值范围;
(2)若这个方程有增根,求k的值.
考点:分式方程的解,分式方程的增根
专题:计算题
分析:(1)分式方程去分母转化为整式方程,求出整式方程的解得到x,根据解为非负数求出k的范围即可;
(2)根据分式方程有增根,得到最简公分母为0,代入整式方程计算即可求出k的值.
(2)根据分式方程有增根,得到最简公分母为0,代入整式方程计算即可求出k的值.
解答:解:(1)分式方程去分母得:x(x-1)-x2+4x-3=k,
去括号合并得:3x-3=k,即x=
,
根据题意得:
≥0,且
≠1且
≠3,
解得:k≥-3,且k≠0,k≠6;
(2)由这个方程有增根,得到x=1或x=3,
将x=1代入整式方程得:k=0;
将x=3代入整式方程得:k=6,
则k的值为0或6.
去括号合并得:3x-3=k,即x=
| k+3 |
| 3 |
根据题意得:
| k+3 |
| 3 |
| k+3 |
| 3 |
| k+3 |
| 3 |
解得:k≥-3,且k≠0,k≠6;
(2)由这个方程有增根,得到x=1或x=3,
将x=1代入整式方程得:k=0;
将x=3代入整式方程得:k=6,
则k的值为0或6.
点评:此题考查了分式方程的解,以及分式方程的增根,弄清题意是解本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
下列条件中不能判定一定是平行四边形的有( )
| A、一组对角相等,一组邻角互补 |
| B、一组对边平行,另一组对边相等 |
| C、一组对边相等,一组对角相等 |
| D、一组对边平行,且一条对角线平分另一条对角 |
 如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.
如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.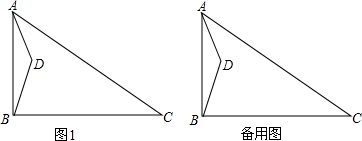
 (1)如图①,请用尺规作图作出圆的一条直径EF(不写作法,保留作图痕迹);
(1)如图①,请用尺规作图作出圆的一条直径EF(不写作法,保留作图痕迹);