题目内容
 如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.
如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.(1)求证:CD=BE.
(2)若AD=3,DC=4,求sin∠ABE的值.
考点:梯形,全等三角形的判定与性质
专题:
分析:(1)证出△ADC≌△CEB,根据全等三角形的性质得出即可;
(2)根据全等三角形性质得出CE=3,BE=4,根据勾股定理求出AC,求出AE,根据勾股定理求出AB,解直角三角形即可.
(2)根据全等三角形性质得出CE=3,BE=4,根据勾股定理求出AC,求出AE,根据勾股定理求出AB,解直角三角形即可.
解答:(1)证明:∵BE⊥AC,
∴∠BEC=∠D=90°,
∵AD∥BC,
∴∠DAC=∠ECB,
在△CDA和△BEC中
∴△CDA≌△BEC(AAS),
∴CD=BE;
(2)解:在Rt△ADC中,由勾股定理得:AC=
=5,
∵△CDA≌△BEC,
∴CE=AD=3,BE=CD=4,
∴AE=5-3=2,
∴在Rt△AEB中,由勾股定理得:AB=
=2
,
∴sin∠ABE=
=
=
.
∴∠BEC=∠D=90°,
∵AD∥BC,
∴∠DAC=∠ECB,
在△CDA和△BEC中
|
∴△CDA≌△BEC(AAS),
∴CD=BE;
(2)解:在Rt△ADC中,由勾股定理得:AC=
| 32+42 |
∵△CDA≌△BEC,
∴CE=AD=3,BE=CD=4,
∴AE=5-3=2,
∴在Rt△AEB中,由勾股定理得:AB=
| 42+22 |
| 5 |
∴sin∠ABE=
| AE |
| AB |
| 2 | ||
2
|
| ||
| 5 |
点评:本题考查了勾股定理,全等三角形的性质和判定,平行线的性质,解直角三角形的应用,题目比较典型,综合性比较强.

练习册系列答案
相关题目
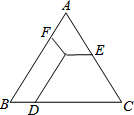 如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )| A、18 | ||
B、9
| ||
| C、6 | ||
| D、条件不够,不能确定 |
 如图,在△ABC中,AB=AC,∠EDF=∠B,求证:△BDE∽△CFD.
如图,在△ABC中,AB=AC,∠EDF=∠B,求证:△BDE∽△CFD. 如图,已知直线
如图,已知直线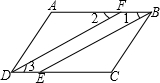 请把下面证明过程补充完整:
请把下面证明过程补充完整: