题目内容
下列条件中不能判定一定是平行四边形的有( )
| A、一组对角相等,一组邻角互补 |
| B、一组对边平行,另一组对边相等 |
| C、一组对边相等,一组对角相等 |
| D、一组对边平行,且一条对角线平分另一条对角 |
考点:平行四边形的判定
专题:
分析:平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定逐一验证.
解答:解:A、能用两组对角相等的四边形是平行四边形判定平行四边形;
B、不能判定平行四边形,如等腰梯形;
C、能用两组对边相等的四边形是平行四边形判定平行四边形;
D、能用两组对边分别平行的四边形是平行四边形判定平行四边形;
故选B.
B、不能判定平行四边形,如等腰梯形;
C、能用两组对边相等的四边形是平行四边形判定平行四边形;
D、能用两组对边分别平行的四边形是平行四边形判定平行四边形;
故选B.
点评:本题考查了平行四边形的判定,熟练掌握相关的定理是解题关键.

练习册系列答案
相关题目
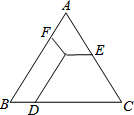 如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
如图,△ABC是等边三角形,P是形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )| A、18 | ||
B、9
| ||
| C、6 | ||
| D、条件不够,不能确定 |
下列运算正确的是( )
| A、a2+a=a3 |
| B、a2•a=a3 |
| C、a2÷a=2 |
| D、(2a)2=4a |
计算:2-3=( )
| A、5 | B、1 | C、-5 | D、-1 |
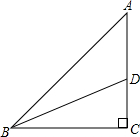 如图,在△ABC中,∠C=90°,点D在AC上,将△BCD沿BD翻折,点C落在斜边AB上,若AC=12cm,DC=5cm,则sinA=
如图,在△ABC中,∠C=90°,点D在AC上,将△BCD沿BD翻折,点C落在斜边AB上,若AC=12cm,DC=5cm,则sinA=