题目内容
9．用圆心角为120°，半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒（如图所示），则这个纸冒的高是（ ）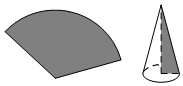
| A． | 3 cm | B． | 2$\sqrt{2}$cm | C． | 3$\sqrt{2}$cm | D． | 4$\sqrt{2}$cm |
分析 设圆锥的底面半径长为xcm，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到2πx=$\frac{120•π•3}{180}$，然后解方程求出x的值后利用勾股定理计算圆锥的高．
解答 解：设圆锥的底面半径长为xcm，
根据题意得2πx=$\frac{120•π•3}{180}$
解得x=1，
所以这个纸冒的高=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$（cm）．
故选B．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
相关题目
如图，已知∠1=80°，∠2=140°，那么∠3=60度．
17．笔盒里有3支笔芯为黑色与2支笔芯为红色的笔，每支笔的笔芯除颜色外均相同．从中任意拿出一支笔，则恰好拿出红色笔芯的笔的概率是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{5}$ |
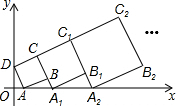在平面直角坐标系中，正方形ABCD的位置如右图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作正方形A1B1C1C；延长C1B1交x轴于点A2，作正方形A2B2C2C1，…按这样的规律进行下去，第2017个正方形的面积为5×（$\frac{3}{2}$）4032．
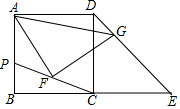正方形ABCD，等腰Rt△CDE，点P是AB上一动点，连接CP，点F是CP的中点，作∠AFG=90°交DE于点G，求证：AF=GF．
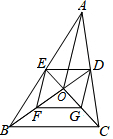如图，在△ABC中，中线BD与CE相交于点O，F、G分别是BO、CO的中点，连接AO，若AO=6，四边形DEFG的周长为14，则BC=（ ）
18．数据-2，-1，0，1，x的平均数为0，则方差为（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{2}$ | D． | $\frac{1}{2}$ |
如图，在△ABC中，∠A=30°，∠B=45°，AC=2，求△ABC的周长和面积．