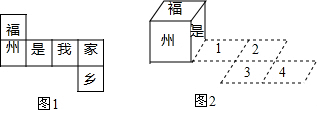
题目内容
17．笔盒里有3支笔芯为黑色与2支笔芯为红色的笔，每支笔的笔芯除颜色外均相同．从中任意拿出一支笔，则恰好拿出红色笔芯的笔的概率是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{5}$ |
分析 直接利用概率公式求解．
解答 解：恰好拿出红色笔芯的笔的概率=$\frac{2}{3+2}$=$\frac{2}{5}$．
故选C．
点评 本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．
练习册系列答案
相关题目
7．下列说法正确的是（ ）
| A． | 百分数都小于1 | |
| B． | 圆的周长是这个圆的半径的3.14倍 | |
| C． | 在含糖7%的糖水中，糖和水的比是7：100 | |
| D． | 如果两个扇形的圆心角相相等，那么半径越长所对的弧长也越长 |
8．计算-5+（-2）×3的结果等于（ ）
| A． | -11 | B． | -1 | C． | 1 | D． | 11 |
5．点A（x1，y1）、B（x2，y2）在函数y=$\frac{6}{x}$的图象上，若0＜x2＜x1，则y1、y2的大小关系是（ ）
| A． | y2＜y1 | B． | y1=y2 | ||
| C． | y1＜y2 | D． | y1、y2的大小关系不确定 |
12．
如图，将矩形ABCD纸片沿EF折叠，若∠DEF=65°，则∠BGE等于（ ）
如图，将矩形ABCD纸片沿EF折叠，若∠DEF=65°，则∠BGE等于（ ）| A． | 110° | B． | 120° | C． | 125° | D． | 130° |
9．用圆心角为120°，半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒（如图所示），则这个纸冒的高是（ ）
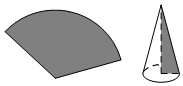
| A． | 3 cm | B． | 2$\sqrt{2}$cm | C． | 3$\sqrt{2}$cm | D． | 4$\sqrt{2}$cm |
6．计算2-3的结果是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 5 |
