题目内容
20.(1)如图①,根据″SAS″,如果BD=CE,∠DBC=∠ECB,那么即可判定△BDC≌△CEB;(2)如图②,BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则根据所学内容,应添加的一个条件为AC=CD.

分析 (1)根据题意知,在△BDC与△CEB中,∠DBC=∠ECB,BC=BC,所以由三角形判定定理SAS可以推知.
(2)可以添加条件AC=CD,再由条件∠BCE=∠ACD,可得∠ACB=∠DCE,再加上条件CB=EC,可根据SAS定理证明△ABC≌△DEC.
解答 解:(1)在△BDC与△CEB中,
$\left\{\begin{array}{l}{BD=CE}\\{∠DBC=∠ECB}\\{BC=BC}\end{array}\right.$,
∴△BDC≌△CEB,
故答案为:∠DBC;∠ECB;
(2)添加条件:AC=CD,
∵∠BCE=∠ACD,
∴∠ACB=∠DCE,
在△ABC和△DEC中$\left\{\begin{array}{l}{BC=EC}\\{∠ACB=∠DCE}\\{AC=DC}\end{array}\right.$,
∴△ABC≌△DEC(SAS),
故答案为:AC=CD(答案不唯一).
点评 本题考查了全等三角形的判定.本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.计算-5+(-2)×3的结果等于( )
| A. | -11 | B. | -1 | C. | 1 | D. | 11 |
15.如果点A(m,n)、B(m-1,n-2)均在一次函数y=kx+b(k≠0)的图象上,那么k的值为( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
5.点A(x1,y1)、B(x2,y2)在函数y=$\frac{6}{x}$的图象上,若0<x2<x1,则y1、y2的大小关系是( )
| A. | y2<y1 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1、y2的大小关系不确定 |
12. 如图,将矩形ABCD纸片沿EF折叠,若∠DEF=65°,则∠BGE等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠DEF=65°,则∠BGE等于( )
 如图,将矩形ABCD纸片沿EF折叠,若∠DEF=65°,则∠BGE等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠DEF=65°,则∠BGE等于( )| A. | 110° | B. | 120° | C. | 125° | D. | 130° |
9.用圆心角为120°,半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒(如图所示),则这个纸冒的高是( )
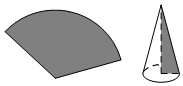

| A. | 3 cm | B. | 2$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
10.下列运算正确的是( )
| A. | 3a2-2a2=1 | B. | $\frac{1}{2}$a•2a2=a2 | C. | a6÷a2=a3 | D. | (-a2b)3÷(a3b)2=-b |
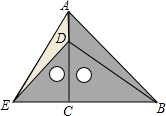 把等腰直角三角板ABC和等腰直角三角板ECD如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
把等腰直角三角板ABC和等腰直角三角板ECD如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.