题目内容
14.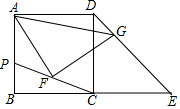 正方形ABCD,等腰Rt△CDE,点P是AB上一动点,连接CP,点F是CP的中点,作∠AFG=90°交DE于点G,求证:AF=GF.
正方形ABCD,等腰Rt△CDE,点P是AB上一动点,连接CP,点F是CP的中点,作∠AFG=90°交DE于点G,求证:AF=GF.
分析 延长AF交DC的延长线于H,连接GH,作GM⊥CD于M,GN⊥AD交AD的延长线于N,CD交AG于O.首先证明△PAF≌△GHF,推出AF=FH,由FG⊥AH,推出GA=GH,由△DCE是等腰直角三角形,推出∠CDE=45°,易证四边形DMGN是正方形,推出GN=GM,可得Rt△ANG≌Rt△HMG,推出∠AGN=∠HGM,推出∠AGH=∠MGN=90°,推出△AGH是等腰直角三角形,即可解决问题.
解答 证明:延长AF交DC的延长线于H,连接GH,作GM⊥CD于M,GN⊥AD交AD的延长线于N,CD交AG于O.
∵四边形ABCD是正方形,
∴AB∥DH,
∴∠PAF=∠GHF,
∵∠AFP=∠HFG,PF=FG,
∴△PAF≌△GHF,
∴AF=FH,
∵FG⊥AH,
∴GA=GH,
∵△DCE是等腰直角三角形,
∴∠CDE=45°,易证四边形DMGN是正方形,
∴GN=GM,
∴Rt△ANG≌Rt△HMG,
∴∠AGN=∠HGM,
∴∠AGH=∠MGN=90°,
∴△AGH是等腰直角三角形,
∴AF=FH,
∴FG=AF=FH.
∴AF=GF.
点评 本题考查正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
4.对于非零的实数a,b,规定a?b=$\frac{1}{b}$$-\frac{1}{a}$,若2?(2x-1)=1,则x=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{6}$ | D. | $-\frac{1}{6}$ |
5.点A(x1,y1)、B(x2,y2)在函数y=$\frac{6}{x}$的图象上,若0<x2<x1,则y1、y2的大小关系是( )
| A. | y2<y1 | B. | y1=y2 | ||
| C. | y1<y2 | D. | y1、y2的大小关系不确定 |
9.用圆心角为120°,半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒(如图所示),则这个纸冒的高是( )
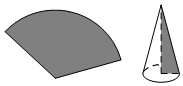

| A. | 3 cm | B. | 2$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
19.某电动自行车厂三月份的产量为1000辆,由于市场需求量不断增大,五月份的产量提高到l210辆,剩该厂四、五月份的月平均增长率为( )
| A. | 12.1% | B. | 20% | C. | 21% | D. | 10% |
6.计算2-3的结果是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
3.下面四个图形中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |