题目内容
19. 如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.
如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.
分析 作CD⊥AB于D,如图,在Rt△ACD中利用含30度的直角三角形三边的关系计算出CD=$\frac{1}{2}$AC=1,AD=$\sqrt{3}$CD=$\sqrt{3}$,在Rt△CBD中,由于∠B=45°,则△ABD为等腰直角三角形,所以BD=CD=1,AB=$\sqrt{2}$CD=$\sqrt{2}$,则AB=BD+AD=1+$\sqrt{3}$,然后根据三角形面积公式计算△ABC的面积.
解答 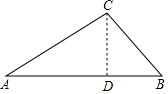 解:作CD⊥AB于D,如图,
解:作CD⊥AB于D,如图,
在Rt△ACD中,∵∠A=30°,
∴CD=$\frac{1}{2}$AC=1,AD=$\sqrt{3}$CD=$\sqrt{3}$,
在Rt△CBD中,∵∠B=45°,
∴BD=CD=1,CB=$\sqrt{2}$AD=$\sqrt{2}$,
∴BA=BD+AD=1+$\sqrt{3}$,
∴△ABC的周长=AB+AC+BC=$\sqrt{2}$+2+1+$\sqrt{3}$=3+$\sqrt{2}+\sqrt{3}$.
△ABC的面积=$\frac{1}{2}$AD•BC=$\frac{1}{2}$•1•($\sqrt{3}$+1)=$\frac{\sqrt{3}+1}{2}$.
答:△ABC的周长为3+$\sqrt{2}+\sqrt{3}$,△ABC的面积为$\frac{\sqrt{3}+1}{2}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
9.用圆心角为120°,半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒(如图所示),则这个纸冒的高是( )
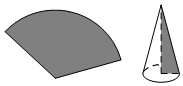

| A. | 3 cm | B. | 2$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
10.下列运算正确的是( )
| A. | 3a2-2a2=1 | B. | $\frac{1}{2}$a•2a2=a2 | C. | a6÷a2=a3 | D. | (-a2b)3÷(a3b)2=-b |
8.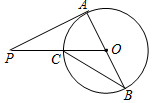 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )
 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )| A. | 27° | B. | 30° | C. | 36° | D. | 54°图3 |