题目内容
1.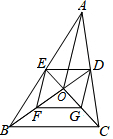 如图,在△ABC中,中线BD与CE相交于点O,F、G分别是BO、CO的中点,连接AO,若AO=6,四边形DEFG的周长为14,则BC=( )
如图,在△ABC中,中线BD与CE相交于点O,F、G分别是BO、CO的中点,连接AO,若AO=6,四边形DEFG的周长为14,则BC=( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 主要考查平行四边形的判定以及三角形中位线的运用,由中位线定理,可得EF∥AO,FG∥BC,且都等于边长BC的一半.分析到此,此题便可解答.
解答 解:∵E、F分别是AB、OB的中点,
∴EF∥AO,EF=$\frac{1}{2}$AO=3,同理DG∥AO,DG=AO=3,
∴四边形DEFG是平行四边形,
∴ED=FG=$\frac{1}{2}$BC=$\frac{14-6}{2}$=4,
∴BC=8.
故选:B.
点评 本题考查了平行四边形的判定和三角形的中位线定理,三角形的中位线的性质定理,为证明线段相等和平行提供了依据.

练习册系列答案
相关题目
12. 如图,将矩形ABCD纸片沿EF折叠,若∠DEF=65°,则∠BGE等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠DEF=65°,则∠BGE等于( )
 如图,将矩形ABCD纸片沿EF折叠,若∠DEF=65°,则∠BGE等于( )
如图,将矩形ABCD纸片沿EF折叠,若∠DEF=65°,则∠BGE等于( )| A. | 110° | B. | 120° | C. | 125° | D. | 130° |
9.用圆心角为120°,半径为3 cm的扇形纸片卷成一个圆锥形无底纸冒(如图所示),则这个纸冒的高是( )
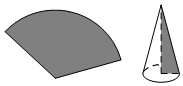

| A. | 3 cm | B. | 2$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | 4$\sqrt{2}$cm |
16.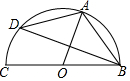 如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )
如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )
 如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )
如图A,D是⊙O上两点,BC是直径.若∠D=35°,则∠OAB的度数是( )| A. | 35° | B. | 55° | C. | 65° | D. | 70° |
6.计算2-3的结果是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 5 |
13.设n为正整数,且n-1<$\sqrt{65}$<n,则n的值为( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
10.下列运算正确的是( )
| A. | 3a2-2a2=1 | B. | $\frac{1}{2}$a•2a2=a2 | C. | a6÷a2=a3 | D. | (-a2b)3÷(a3b)2=-b |