题目内容

若a，b是方程x2-2x-1=0的两个实数根，则代数式（a-b）（a+b-2）+ab=
 
．
考点：根与系数的关系
专题：
分析：由根与系数的关系得出a+b=2，ab=-1，再将它们代入（a-b）（a+b-2）+ab，计算即可求解．
解答：解：∵a，b是方程x2-2x-1=0的两个实数根，
∴a+b=2，ab=-1，
∴（a-b）（a+b-2）+ab=（a-b）（2-2）+（-1）=-1．
故答案为-1．
点评：本题考查了根与系数的关系：x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q．利用整体代入是解题的关键．
练习册系列答案
相关题目
在△ABC中，AD=BD，F是高AD和BE的交点，求证：BF=AC．
已知在纸面上有一数轴（如图），折叠纸面．
（1）若表示数1的点与表示数-1的点重合，则表示-2的点与表示数
 
的点重合；
（2）若表示数-1的点与表示数3的点重合，回答以下两个问题：
①表示数5的点与表示数
 
的点重合；
②若数轴上A、B两点之间的距离为m（A在B的左侧），且A、B两点经折叠后重合，直接写出A、B两点表示的数（用含m的式子表示）是多少？
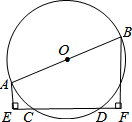如图，AB是⊙O的直径，CD是弦，若AB=10cm，CD=8cm，那么A、B两点到直线CD的距离之和为（　　）
A、12cmB、10cm
C、8cmD、6cm
问题背景：
设一元二次方程ax2+bx+c=0 （a≠0）两个根分别是x1，x2
则x1+x2=-
b
a
，x1x2=
c
a

（1）若x1：x2=2：1时，求
b2
ac
的值

类比探究：
（2）若x1：x2=1：1时，则
b2
ac
=
 

（3）若x1：x2=3：1时，则
b2
ac
=
 

（4）若x1：x2=m：1时，则
b2
ac
=
 
 （用m的式子表示）
拓展延伸：
（5）若x1：x2=m：n时，则
b2
ac
=
 
．
在△ABC中，∠A=64°，圆O交AB边于G，H，交BC边于M，N，交AC边于K，L，且GH=MN=KL，连接OB，OC，求∠BOC的度数．
把函数y=-2x2+4x+3用配方法配成顶点式，并写出它的对称轴和顶点坐标．
若a，b互为相反数，x，y互为倒数，xy≠0，则（a+b）
x
y
+xy=（　　）
A、-1B、0C、1D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网