题目内容
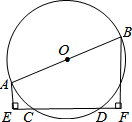 如图,AB是⊙O的直径,CD是弦,若AB=10cm,CD=8cm,那么A、B两点到直线CD的距离之和为( )
如图,AB是⊙O的直径,CD是弦,若AB=10cm,CD=8cm,那么A、B两点到直线CD的距离之和为( )| A、12cm | B、10cm |
| C、8cm | D、6cm |
考点:垂径定理,勾股定理,梯形中位线定理
专题:
分析:要求A、B两点到直线CD的距离之和,只需作弦的弦心距,即为梯形的中位线,根据垂径定理和勾股定理求得此弦心距;再根据梯形的中位线定理进行求解.
解答: 解:作OG⊥EF,连接OD,
解:作OG⊥EF,连接OD,
∴G为CD中点,
∵CD=8cm,
则DG=
CD=4cm.
∵AB=10cm,
∴OD=
AB=5cm,
所以OG=
=3cm.
根据梯形中位线定理,得A、B两点到直线CD的距离之和为3×2=6(cm).
故选D.
 解:作OG⊥EF,连接OD,
解:作OG⊥EF,连接OD,∴G为CD中点,
∵CD=8cm,
则DG=
| 1 |
| 2 |
∵AB=10cm,
∴OD=
| 1 |
| 2 |
所以OG=
| 52-42 |
根据梯形中位线定理,得A、B两点到直线CD的距离之和为3×2=6(cm).
故选D.
点评:此题主要考查了垂径定理,注意此题中常见的辅助线:作弦的弦心距.综合运用垂径定理、勾股定理以及梯形的中位线定理.

练习册系列答案
相关题目
关于x的一元二次方程的两个根x1=-1,x2=-3,则这个方程是( )
| A、x2+4x+3=0 |
| B、x2+4x-3=0 |
| C、x2-4x-3=0 |
| D、x2-4x+3=0 |
已知(a2+b2)(a2+b2-9)-10=0,则a2+b2的值为( )
| A、-1 | B、10 |
| C、-1或10 | D、-1和10 |
 如果表示a、b的实数的点在数轴上的位置如图所示,那么化简|a-b|+
如果表示a、b的实数的点在数轴上的位置如图所示,那么化简|a-b|+ 如图,AB为⊙O的切线,AC、BD分别与⊙O切于C、D点,若AB=5,AC=3,则BD的长是
如图,AB为⊙O的切线,AC、BD分别与⊙O切于C、D点,若AB=5,AC=3,则BD的长是