题目内容
7. 已知,如图△ABC中,CD⊥AB于D,BE⊥AC于E,若BD=CD,求证:BF=AC.
已知,如图△ABC中,CD⊥AB于D,BE⊥AC于E,若BD=CD,求证:BF=AC.
分析 根据在△ABC中,CD⊥AB于D,BE⊥AC于E,可以求得∠BDF=∠CDA=90°,∠FEA=90°,从而可以求得∠DBF与∠DCA的关系,进而可以证明△BDF和△CDA全等,从而可以证明BF=AC.
解答 证明:∵在△ABC中,CD⊥AB于D,BE⊥AC于E,
∴∠BDF=∠CDA=90°,∠FEA=90°,
∴∠A+∠DBF=90°,∠A+∠DCA=90°,
∴∠DBF=∠DCA,
在△BDF和△CDA中,
$\left\{\begin{array}{l}{∠BDF=∠CDA}\\{BD=CD}\\{∠DBF=∠DCA}\end{array}\right.$,
∴△BDF≌△CDA(ASA),
∴BF=AC.
点评 本题考查全等三角形的判定和性质,解题的关键是找出三角形全等的条件.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
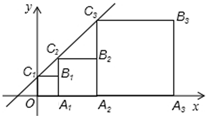 正方形OA1B1C1、正方形A1A2B2C2和正方形A2A3B3C3按如图所示方式放置,点C1、C2、C3在直线y=x+1上,点A1、A2、A3在x轴上,已知C1点的坐标是(0,1),则B3的坐标为(7,4).
正方形OA1B1C1、正方形A1A2B2C2和正方形A2A3B3C3按如图所示方式放置,点C1、C2、C3在直线y=x+1上,点A1、A2、A3在x轴上,已知C1点的坐标是(0,1),则B3的坐标为(7,4).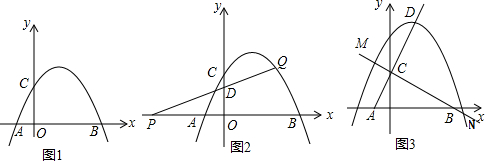
 如图,△ACB与△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,请你尝试发现线段AD与BE的数量、位置关系.
如图,△ACB与△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,请你尝试发现线段AD与BE的数量、位置关系. 如图,AB∥CD,AB=CD,∠A=∠C.你能得到哪些有关角、边的结论?△ABF与△CDE全等吗?
如图,AB∥CD,AB=CD,∠A=∠C.你能得到哪些有关角、边的结论?△ABF与△CDE全等吗?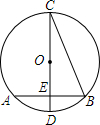 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC.若AB=2,∠BCD=30°,则⊙O的半径为$\frac{2\sqrt{3}}{3}$.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC.若AB=2,∠BCD=30°,则⊙O的半径为$\frac{2\sqrt{3}}{3}$.