题目内容
19. 如图,AB∥CD,AB=CD,∠A=∠C.你能得到哪些有关角、边的结论?△ABF与△CDE全等吗?
如图,AB∥CD,AB=CD,∠A=∠C.你能得到哪些有关角、边的结论?△ABF与△CDE全等吗?
分析 由AB∥CD,根据平行线的性质,可证得∠B=∠D,然后利用ASA可判定△ABF与△CDE全等,则可证得对应角相等,对应边相等.
解答 解:角:∠AFB=∠CED,∠AFD=∠CEB,边:AF=CE,BF=DE,△ABF与△CDE全等.
理由:∵AB∥CD,
∴∠B=∠D,
在△ABF和△CDE中,
$\left\{\begin{array}{l}{∠A=∠C}\\{AB=CD}\\{∠B=∠D}\end{array}\right.$,
∴△ABF≌△CDE(ASA),
∴∠AFB=∠CED,AF=CE,BF=DE,
∴∠AFD=∠CEB.
点评 此题考查了全等三角形的判定与性质以及平行线的性质.注意利用平行线的性质,证得角相等是解此题的关键.

练习册系列答案
相关题目
9.若9x2+kxy+4y2是一个完全平方式,则k的值为( )
| A. | 6 | B. | ±6 | C. | 12 | D. | ±12 |
 已知,如图△ABC中,CD⊥AB于D,BE⊥AC于E,若BD=CD,求证:BF=AC.
已知,如图△ABC中,CD⊥AB于D,BE⊥AC于E,若BD=CD,求证:BF=AC.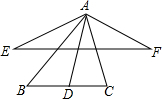 如图,在△ABC中,AD为BC边上的中线,若∠BAC<90°,作EA⊥AC,FA⊥BA,且AE=AC,AF=AB.连接EF,写出AD与EF的数量关系,并证明.
如图,在△ABC中,AD为BC边上的中线,若∠BAC<90°,作EA⊥AC,FA⊥BA,且AE=AC,AF=AB.连接EF,写出AD与EF的数量关系,并证明.
 如图,四边形OACB中,CM⊥OA,∠A+∠B=180°,OA+OB=2OM,CA=CB.求证:OC平分∠AOB.
如图,四边形OACB中,CM⊥OA,∠A+∠B=180°,OA+OB=2OM,CA=CB.求证:OC平分∠AOB.