Question

17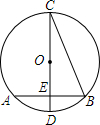．如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC．若AB=2，∠BCD=30°，则⊙O的半径为$\frac{2\sqrt{3}}{3}$．

Answer 1

分析 连接OB，根据垂径定理求出BE，由圆周角定理求出∠BOE=60°，解直角三角形求出OB即可．

解答 解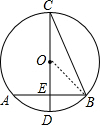：连接OB，如图所示：
∵∠BCD=30°，
∴∠BOE=2∠BCD=60°，
∵直径CD⊥弦AB，AB=2，
∴BE=$\frac{1}{2}$AB=1，∠OEB=90°，
∴OB=$\frac{BE}{sin60°}$=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$，
即⊙O的半径为$\frac{2\sqrt{3}}{3}$．
故答案为：$\frac{2\sqrt{3}}{3}$．

点评 本题考查了垂径定理，圆周角定理，解直角三角形；能根据垂径定理求出BE和解直角三角形求出OB长是解此题的关键，难度适中．