题目内容
11．
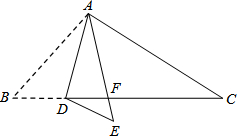如图，在△ABC中，点D是BC边上的一点，∠B=50°，∠BAD=30°，将△ABD沿AD折叠得到△AED，AE与BC交于点F．则∠EDF的度数是20°．
分析 先根据折叠性质得：∠BAD=∠EAD=30°，∠E=∠B=50°，再根据外角定理求∠AFC=110°，由三角形内角和可以得出∠EDF为20°．
解答 解：由折叠得：∠BAD=∠EAD=30°，∠E=∠B=50°，
∵∠B=50°，
∴∠AFC=∠B+∠BAE=50°+60°=110°，
∴∠DFE=∠AFC=110°，
∴∠EDF=180°-∠E-∠DFE=180°-50°-110°=20°，
故答案为：20°．
点评 本题是折叠问题，考查了折叠的性质和外角定理：①折叠前后的两个角对应相等；②三角形的一个外角等于与它不相邻的两个内角的和；与对顶角性质和三角形内角和定理求出角的度数．
练习册系列答案
同步练习强化拓展系列答案
相关题目
如图，在四边形ABCD中，∠ACB=∠ADB=90°，E、F分别是AB、AD的中点，则EF与CD有什么关系？
如图所示，作字母“E”关于y轴对称的图形，并写出所得图形相应各点的坐标．
如图所示，在一次“寻宝”游戏中，已知寻宝图上两个标志点A（-3，0）和点B（5，0），宝藏分别埋在C（3，4）和D（-2，3）两点．请你首先建立直角坐标系确定宝藏的位置，然后在图上标出“宝藏”的位置并计算出四边形ABCD的面积．
如图所示，在△ABC中，∠B=70°，∠C=60°，直线DE交AC于点D，交AB于点E，如果∠1=95°，则∠2=145°．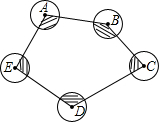
如图，五个半径为2的圆，圆心分别是点A，B，C，D，E，则图中阴影部分的面积和是多少？（S扇形=$\frac{nπR^2}{360°}$）