题目内容
20.在△ABC中,已知a=2$\sqrt{2}$,b=$\sqrt{3}$,∠C=60°,则△ABC的面积为$\frac{3\sqrt{2}}{2}$.分析 根据题意,先画出图形,再根据三角形的面积的求法,直接得出答案即可.
解答 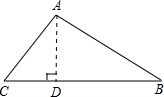 解:过点A作AD⊥BC,垂足为D,
解:过点A作AD⊥BC,垂足为D,
∵a=2$\sqrt{2}$,b=$\sqrt{3}$,∠C=60°,
∴∠CAD=30°,
∴CD=$\frac{1}{2}$$\sqrt{3}$,
∴AD=$\frac{1}{2}$$\sqrt{3}$×$\sqrt{3}$=$\frac{3}{2}$,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×2$\sqrt{2}$×$\frac{3}{2}$=$\frac{3\sqrt{2}}{2}$,
故答案为$\frac{3\sqrt{2}}{2}$.
点评 本题考查了二次根式的应用,掌握二次根式的化简和三角形的面积是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
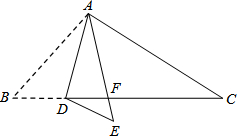 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.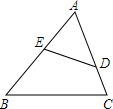 如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长. 已知:如图,PM=PN,∠M=∠N.求证:AM=BN.
已知:如图,PM=PN,∠M=∠N.求证:AM=BN.