题目内容
3.在矩形ABCD中,对角线BD与边BC所构成的锐角∠DBC=30°,已知DC=2cm,则该矩形的面积是4$\sqrt{3}$cm2.分析 由矩形的性质得出∠C=90°,求出BD=2CD=4cm,由勾股定理得出BC的长,即可求出矩形的面积.
解答 解:∵四边形ABCD是矩形,
∴∠C=90°,
∵∠DBC=30°,
∴BD=2CD=4cm,
∴BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=2$\sqrt{3}$cm,
∴矩形ABCD的面积=BC•CD=2$\sqrt{3}$×2=4$\sqrt{3}$(cm2);
故答案为:4$\sqrt{3}$.
点评 本题考查了矩形的性质、含30°角的直角三角形的性质、勾股定理;熟练掌握矩形的性质,由勾股定理求出BC是解决问题的关键.

练习册系列答案
相关题目
 如图,将长、宽分别为40cm,20cm的长方形玻璃裁成两部分,然后拼成一个直角三角形,画出图形,并注明各边的长度.
如图,将长、宽分别为40cm,20cm的长方形玻璃裁成两部分,然后拼成一个直角三角形,画出图形,并注明各边的长度.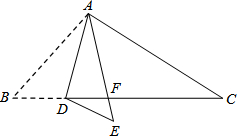 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.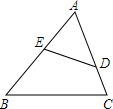 如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.
如图,D、E分别是AC、AB上的点,△ADE∽△ABC,且DE=4,BC=12,CD=9,AD=3,求AE、BE的长.