题目内容
4. 如图,在四边形ABCD中,∠ACB=∠ADB=90°,E、F分别是AB、AD的中点,则EF与CD有什么关系?
如图,在四边形ABCD中,∠ACB=∠ADB=90°,E、F分别是AB、AD的中点,则EF与CD有什么关系?
分析 连接DE,根据直角三角形的性质可得出DE=CE=$\frac{1}{2}$AB,由点E是CD的中点可得出结论.
解答  解:EF⊥CD.
解:EF⊥CD.
理由:连接DE,
∵∠ACB=∠ADB=90°,点E是AB的中点,
∴DE=CE=$\frac{1}{2}$AB.
∵点E是CD的中点,
∴EF⊥CD.
点评 本题考查的是直角三角形及等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
12.A,B两地盛产桃,A地有桃400吨,B地有桃300吨.现将这些桃运到C、D两个冷藏仓库,已知C仓库可储存320吨,D仓库可储存380吨;从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从A地运往C仓库的桃重量为x吨,A、B两地运往两仓库的桃运输费用分别为yA元和yB元.
(1)请填写下表后分别求出yA,yB与x之间的函数关系式,并写出定义域.
(2)试讨论A,B两地中,哪个运费较少?
(1)请填写下表后分别求出yA,yB与x之间的函数关系式,并写出定义域.
| 仓库 产地 | C | D | 总计 |
| A | x吨 | 400吨 | |
| B | 300吨 | ||
| 总计 | 320吨 | 380 | 700吨 |
 如图,A、B、C都在⊙O上,∠1=∠B,求证:AE是⊙O的切线.
如图,A、B、C都在⊙O上,∠1=∠B,求证:AE是⊙O的切线.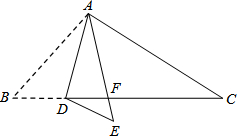 如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.
如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.则∠EDF的度数是20°.