题目内容
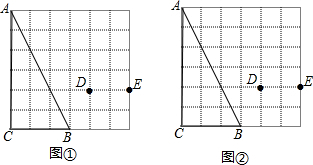
14．图①、图②是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形顶点叫做格点，△ABC的顶点在格点上，点D、E在格点上，连结DE．（1）在图①、图②中分别找到不同的格点F，使以D、E、F为顶点的三角形与△ABC相似，并画出△DEF（每个网格中只画一个即可）．
（2）使△DEF与△ABC相似的格点F一共有6个．
分析 （1）利用相似三角形的性质得出符合题意的答案；
（2）利用（1）中所画图形得出所有的可能．
解答 
解：（1）如图所示：
（2）如图①所示：使△DEF与△ABC相似的格点F一共有6个．
故答案为：6．
点评 此题主要考查了相似变换，根据题意正确利用相似三角形的性质得出对应边的长是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．
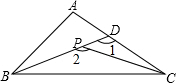如图，P是△ABC内一点，延长CP交AB于D，则下列不等式成立的是（ ）
如图，P是△ABC内一点，延长CP交AB于D，则下列不等式成立的是（ ）| A． | ∠2＞∠A＞∠1 | B． | ∠2＞∠1＞∠A | C． | ∠1＞∠A＞∠2 | D． | ∠A＞∠1＞∠2 |
5．
实数x、y、z在数轴上的位置如图所示，则下列关系正确的是（ ）
实数x、y、z在数轴上的位置如图所示，则下列关系正确的是（ ）| A． | x+y+z＞0 | B． | x+y+z＜0 | C． | xy＜yz | D． | xy＜xz |
2．
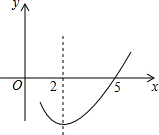二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（5，0），对称轴为直线x=2，则下列结论中正确的是（ ）
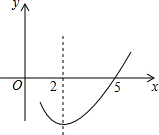二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（5，0），对称轴为直线x=2，则下列结论中正确的是（ ）| A． | 当x＞2时，y随x增大而减小 | B． | 4a=b | ||
| C． | 图象过点（-1，0） | D． | 9a+3b+c＞0 |
9．
如图，AD、BC相交于点O，AB∥CD，若$\frac{AO}{OD}=\frac{2}{3}$，则$\frac{AB}{CD}$的值是（ ）
如图，AD、BC相交于点O，AB∥CD，若$\frac{AO}{OD}=\frac{2}{3}$，则$\frac{AB}{CD}$的值是（ ）| A． | $\frac{2}{5}$ | B． | $\frac{3}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{4}{9}$ |
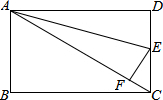已知：如图，长方形ABCD中，AB=6，AD=8，沿直线AE把△ADE折叠，点O恰好落在AC上一点F处．