题目内容
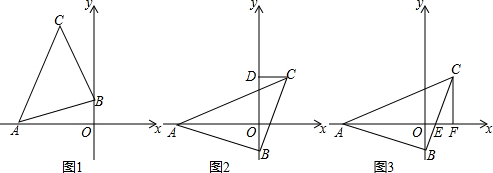
16.已知,△ABC是等腰直角三角形,BC=AB,A点在x轴负半轴上,直角顶点B在y轴上,点C在x轴上方.(1)如图1所示,若A的坐标是(-3,0),点B的坐标是(0,1),求点C的坐标;
(2)如图2,过点C作CD⊥y轴于D,求证OA=CD+OD;
(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问CF与AE有怎样的数量关系?并说明理由.
分析 (1)先求出OA=3,OB=1,再判断出AB=CB,∠BAO=∠CBH,进而得出△AOB≌△BHC,即可得出结论;
(2)同(1)的方法即可得出结论;
(3)先判断出∠CBD=90°,再判断出∠BCD=∠DAF,进而判断出△ABE≌△CBD,得出AE=CD,最后判断出DF=CF即可得出结论、
解答 解:(1)如图1,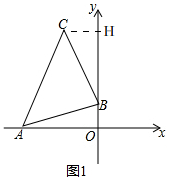 过点C作CH⊥y轴于H,
过点C作CH⊥y轴于H,
∵A(-3,0),B(0,1),
∴OA=3,OB=1,
∵△ABC是等腰直角三角形,
∴AB=CB,∠ABC=90°,
∴∠ABO+∠CBH=90°,
∵∠ABO+∠BAO=90°,
∴∠BAO=∠CBH,
在△AOB和△BHC中,$\left\{\begin{array}{l}{∠AOB=∠BHC=90°}\\{∠BAO=∠CBH}\\{AB=CB}\end{array}\right.$,
∴△AOB≌△BHC,
∴CH=OB=1,BH=OA=3,
∴OH=OB+BH=4,
∴C(-1,4);
(2)∵△ABC是等腰直角三角形,
∴AB=CB,∠ABC=90°,
∴∠ABO+∠CBD=90°,
∵∠ABO+∠BAO=90°,
∴∠BAO=∠CBD,
在△AOB和△BDC中,$\left\{\begin{array}{l}{∠AOB=∠BHC=90°}\\{∠BAO=∠CBH}\\{AB=CB}\end{array}\right.$,
∴△AOB≌△BDC,
∴CD=OB,BD=OA,
∵BD=OB+OD=CD+OD,
∴OA=CD+OD;
(3)CF=$\frac{1}{2}$AE,
理由:如图3,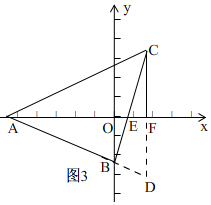 延长CF,AB相交于点D,
延长CF,AB相交于点D,
∴∠CBD=180°-∠ABC=90°,
∵CF⊥x轴,
∴∠BCD+∠D=90°,
∵∠DAF+∠D=90°,
∴∠BCD=∠DAF,
在△ABE和△CBD中,$\left\{\begin{array}{l}{∠ABE=∠CBD}\\{∠BAE=∠BCD}\\{AB=CB}\end{array}\right.$,
∴△ABE≌△CBD,
∴AE=CD,
∵x轴平分∠BAC,CF⊥x轴,
∴AC=AD,
∵CF⊥x轴,
∴CF=DF,
∴CF=$\frac{1}{2}$CD=$\frac{1}{2}$AE.
点评 此题是三角形综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,角平分线的定义,解本题的关键是构造全等三角形,是一道中等难度的中考常考题.

| A. | 正数 | B. | 负数 | C. | 非负数 | D. | 非正数 |
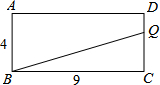 如图,长方形ABCD中,AB=4,BC=9,动点Q沿着C→D→A→B的方向运动至点B停止,设点Q运动的路程为x,△QCB的面积为y.
如图,长方形ABCD中,AB=4,BC=9,动点Q沿着C→D→A→B的方向运动至点B停止,设点Q运动的路程为x,△QCB的面积为y.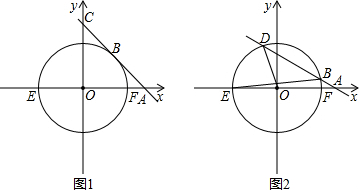
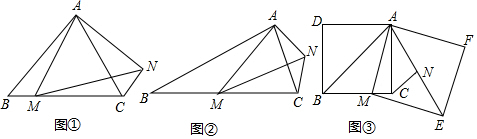
 如图,将边长为4的正方形ABCD沿其对角线AC剪开,固定△ADC,并把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为2时,它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$.
如图,将边长为4的正方形ABCD沿其对角线AC剪开,固定△ADC,并把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为2时,它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$.