题目内容
 如图,在圆内接四边形ABCD中,BC=DC,求证:CA2-CB2=AB•AD.
如图,在圆内接四边形ABCD中,BC=DC,求证:CA2-CB2=AB•AD.考点:全等三角形的判定与性质,角平分线的性质,勾股定理,圆心角、弧、弦的关系
专题:证明题
分析:连接AC,作CM⊥AB的延长线于M,CN⊥AD于N,根据同圆中,等弦对等弧,等弧对等角得出∠BAC=∠DAC,根据圆内接四边形的性质求得∠ADC=∠CBM,然后根据AAS求得△CBM≌△CDN(AAS),得出CM=CN;BM=DN,进而根据HL求得△ACM≌△ACN求得AM=AN,从而求得AD=AB+2BM,根据勾股定理得出BC2=CM2+BM2…①,AC2=AM2+CM2=(AB+BM)2+CM2…②,②-①即可求得结论.
解答: 证明:如图所示:连接AC,作CM⊥AB的延长线于M,CN⊥AD于N
证明:如图所示:连接AC,作CM⊥AB的延长线于M,CN⊥AD于N
∵BC=DC;
∴
=
∴∠BAC=∠DAC,
又∠ABC+∠ADC=∠ABC+∠CBM=180°,
∴∠ADC=∠CBM,
在△CBM与△CDN中,
,
∴△CBM≌△CDN(AAS),
∴CM=CN;BM=DN,
在RT△ACM与RT△ACN中,
,
∴△ACM≌△ACN(HL),
∴AM=AN,
∴AD=AN+DN=AM+DN=AB+BM+BM=AB+2BM,
在Rt△BCM中有:BC2=CM2+BM2…①
在Rt△ACM中有:AC2=AM2+CM2=(AB+BM)2+CM2…②
②-①得:AC2-BC2=AB2+2AB•BM=AB(AB+2BM)=AB•AD,
即CA2-CB2=AB•AD.
 证明:如图所示:连接AC,作CM⊥AB的延长线于M,CN⊥AD于N
证明:如图所示:连接AC,作CM⊥AB的延长线于M,CN⊥AD于N∵BC=DC;
∴
 |
| BC |
 |
| DC |
∴∠BAC=∠DAC,
又∠ABC+∠ADC=∠ABC+∠CBM=180°,
∴∠ADC=∠CBM,
在△CBM与△CDN中,
|
∴△CBM≌△CDN(AAS),
∴CM=CN;BM=DN,
在RT△ACM与RT△ACN中,
|
∴△ACM≌△ACN(HL),
∴AM=AN,
∴AD=AN+DN=AM+DN=AB+BM+BM=AB+2BM,
在Rt△BCM中有:BC2=CM2+BM2…①
在Rt△ACM中有:AC2=AM2+CM2=(AB+BM)2+CM2…②
②-①得:AC2-BC2=AB2+2AB•BM=AB(AB+2BM)=AB•AD,
即CA2-CB2=AB•AD.
点评:本题考查了圆周角、弦、弧的关系,三角形全等的判定和性质,勾股定理的应用,作出辅助线构建直角三角形是本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,BF=FE,DF与AC相交于点M,求证:AM=MC.
如图,在△ABC中,∠ACB=90°,∠BAC=30°,△ABE和△ACD都是等边三角形,BF=FE,DF与AC相交于点M,求证:AM=MC.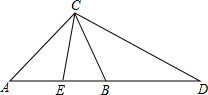 如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.
如图,CE、CB分别是△ABC与△ADC的中线,且∠ACB=∠ABC.求证:CD=2CE.