题目内容
已知一次函数y=kx+b的图象经过点A(3,-3),且与直线y=4x-3的交点B在x轴上.
(1)求直线AB解析式;
(2)求直线AB与坐标轴所围成的△AOB(O为坐标原点)的面积.
(1)求直线AB解析式;
(2)求直线AB与坐标轴所围成的△AOB(O为坐标原点)的面积.
考点:两条直线相交或平行问题,一次函数图象上点的坐标特征
专题:
分析:(1)根据一次函数y=kx+b的图象与直线y=4x-3的交点B在x轴上,把y=0代入直线y=4x-3中求出x的值,确定出B坐标,将A与B坐标代入求出k与b的值,即可确定出直线AB解析式;
(2)根据直线的解析式先求得直线与y轴的交点坐标,然后根据三角形的面积公式即可求解.
(2)根据直线的解析式先求得直线与y轴的交点坐标,然后根据三角形的面积公式即可求解.
解答:解:∵一次函数y=kx+b的图象与直线y=4x-3的交点B在x轴上,
∴将y=0代入y=4x-3得:x=
,即B(
,0),
把A(3,-3),B(
,0)代入得:
,
解得:
.
则直线AB解析式为y=-
x+1.
(2)∵直线AB解析式为y=-
x+1,
∴直线AB与y轴的交点C(0,1),
∴OB=
,OC=1,
∴S△OBC=
OB•OC=
×
×1=
.
即直线AB与坐标轴所围成的△AOB(O为坐标原点)的面积为
.
∴将y=0代入y=4x-3得:x=
| 3 |
| 4 |
| 3 |
| 4 |
把A(3,-3),B(
| 3 |
| 4 |
|
解得:
|
则直线AB解析式为y=-
| 4 |
| 3 |
(2)∵直线AB解析式为y=-
| 4 |
| 3 |
∴直线AB与y轴的交点C(0,1),
∴OB=
| 3 |
| 4 |
∴S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
即直线AB与坐标轴所围成的△AOB(O为坐标原点)的面积为
| 3 |
| 8 |
点评:此题考查了用待定系数法求函数解析式和根据图象与坐标轴的交点求直线与两坐标轴围成三角形的面积,属于基础题.

练习册系列答案
相关题目
 如图,在圆内接四边形ABCD中,BC=DC,求证:CA2-CB2=AB•AD.
如图,在圆内接四边形ABCD中,BC=DC,求证:CA2-CB2=AB•AD.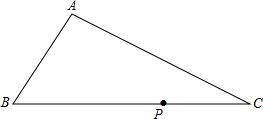 如图,在△ABC中,∠A=90°,∠C=30°,AB=2.5,定点P在斜边BC上,且BP=3,以P点为中心,将△ABC按逆时针方向旋转90°至△A′B′C′.
如图,在△ABC中,∠A=90°,∠C=30°,AB=2.5,定点P在斜边BC上,且BP=3,以P点为中心,将△ABC按逆时针方向旋转90°至△A′B′C′.