Question

如图，在△ABC中，∠ACB=90°，∠BAC=30°，△ABE和△ACD都是等边三角形，BF=FE，DF与AC相交于点M，求证：AM=MC．

Answer 1

考点：平行四边形的判定与性质,等边三角形的性质,菱形的判定与性质

专题：证明题

分析：连接AF、FC，根据等边三角形的性质可得AF是∠BAE的平分线，然后求出∠BAF=∠BAC=30°，再利用“角角边”证明△ABF和△ABC全等，根据全等三角形对应边相等可得AF=AC，然后求出△AFC是等边三角形，再根据等边三角形的性质求出AF=FC=CD=AD=AC，然后求出四边形AFCD是菱形，根据菱形的对角线互相平分可得AM=MC．

解答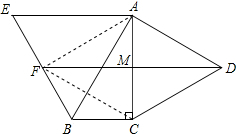：证明：如图，连AF，FC，
∵△ABE是等边三角形，BF=EF，
∴AF是∠BAE的平分线，
∴∠BAF=∠BAE=

1

2

×60°=30°，
∵∠BAC=30°，
∴∠BAF=∠BAC=30°，
在△ABF和△ABC中，

∠BAF=∠BAC ∠AFB=∠ACB=90° AB=AB

，
∴△ABF≌△ABC（AAS），
∴AF=AC，
∵∠FAC=∠BAF+∠BAC=30°+30°=60°，
∴△AFC是等边三角形，
又∵△ACD是等边三角形，
∴AF=FC=CD=AD=AC，
∴四边形AFCD是菱形，
∴AM=MC．

点评：本题考查了菱形的判定与性质，等边三角形的性质，全等三角形的判定与性质，作辅助线构造出全等三角形和菱形是解题的关键，也是本题的难点．