题目内容
12.已知∠BAC=90°,半径为r的圆O与两条直角边AB,AC都相切,设AB=a(a>r),BE与圆O相切于点E.现给出下列命题:①当∠ABE=60°时,BE=$\sqrt{3}r$; ②当∠ABE=90°时,BE=r;则下列判断正确的是( )| A. | 命题①是真命题,命题②是假命题 | B. | 命题①②都是真命题 | ||
| C. | 命题①是假命题,命题②是真命题 | D. | 命题①②都是假命题 |
分析 ①如图1,根据切线的性质得出BE=BF,OE⊥BE,OF⊥AB,进一步求得RT△OBF≌RT△OBE,得出∠OBE=∠OBF=$\frac{1}{2}$∠ABE=30°,解直角三角形即可求得BE=$\sqrt{3}r$;
②根据切线的性质得出BE=BF,OE⊥BE,OF⊥AB,根据题意证得四边形BEDF是正方形,得出BE=r.
解答 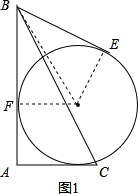 解:①如图1,∵AB和BE是圆O的切线,
解:①如图1,∵AB和BE是圆O的切线,
∴BE=BF,OE⊥BE,OF⊥AB,
在RT△OBF和RT△OBE中,
$\left\{\begin{array}{l}{BE=BF}\\{OB=OB}\end{array}\right.$,
∴RT△OBF≌RT△OBE(HL),
∴∠OBE=∠OBF=$\frac{1}{2}$∠ABE=30°,
∴BE=cot30°•OE=$\sqrt{3}$r;
②如图2,∵AB和BE是圆O的切线,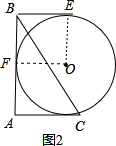
∴BE=BF,OE⊥BE,OF⊥AB,
∵∠ABE=90°,
∴四边形BEDF是正方形,
∴BE=OE
∴BE=r.
故命题①②都是真命题.
故选B.
点评 本题考查了切线的性质,命题和定理,三角形全等的判定和性质,正方形的判定和性质,切线长定理的应用是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
17.下列运算正确的是( )
| A. | -5(a-1)=-5a+1 | B. | a2+a2=a4 | C. | 3a3•2a2=6a6 | D. | (-a2)3=-a6 |
1.运用等式性质的变形,正确的是( )
| A. | 如果a=b,那么a+c=b-c | B. | 如果$\frac{a}{c}=\frac{b}{c}$,那么a=b | ||
| C. | 如果a=b,那么$\frac{a}{c}=\frac{b}{c}$ | D. | 如果a=3,那么a2=3a2 |
2.下列计算正确的是( )
| A. | ($\frac{1}{2}$)0=$\frac{1}{2}$ | B. | (-2)-1=$\frac{1}{2}$ | C. | -2×(-5)=10 | D. | 2-3=1 |
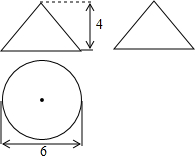 已知某几何体的三视图如图所示(单位:cm),则它的侧面展开图的面积是15πcm2.
已知某几何体的三视图如图所示(单位:cm),则它的侧面展开图的面积是15πcm2.