题目内容
16．
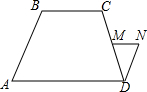如图，在梯形ABCD中，AD∥BC，M是CD中点，MN∥AD，DN∥AB，设BC=a，AD=b（a＜b），那么MN与a、b有怎样的数量关系．试加以证明．
分析 延长NM交AB于点H，易证四边形ADNH是平行四边形，由平行四边形的性质以及梯形中位线的性质即可得到MN与a、b之间的数量关系．
解答 解：MN=$\frac{b-a}{2}$，理由如下：
延长NM交AB于点H，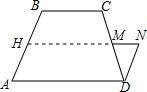
∵AD∥BC，MN∥AD，DN∥AB，
∴四边形ADNH是平行四边形，
∴AD=HN，
∵M是CD中点，HN∥BC∥AD，
∴HM是梯形ABCD的中位线，
∴HM=$\frac{a+b}{2}$，
∵MN=HN-HM=AD-HM，BC=a，AD=b（a＜b），
∴MN=b-$\frac{a+b}{2}$=$\frac{b-a}{2}$．
点评 本题考查了平行四边形的判定和性质以及梯形中位线的性质，解题的关键是熟记特殊几何图形的各种性质．
练习册系列答案
相关题目
如图，已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上，且点A的横坐标为$\frac{\sqrt{5}-1}{2}$，S矩形ABCD=2$\sqrt{5}$，则k=1．
1．运用等式性质的变形，正确的是（ ）
| A． | 如果a=b，那么a+c=b-c | B． | 如果$\frac{a}{c}=\frac{b}{c}$，那么a=b | ||
| C． | 如果a=b，那么$\frac{a}{c}=\frac{b}{c}$ | D． | 如果a=3，那么a2=3a2 |