题目内容
8. 如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数y2=$\frac{k}{x}$(k为常数,k≠0)的图象相交于点A(1,3)、B(-3,n).
如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数y2=$\frac{k}{x}$(k为常数,k≠0)的图象相交于点A(1,3)、B(-3,n).(1)求这两个函数的解析式及其图象的另一交点B的坐标;
(2)观察图象,写出使函数值0>y1≥y2的自变量x的取值范围.
分析 (1)把A的坐标分别代入y1=x+m、y2=$\frac{k}{x}$,由待定系数法即可求得解析式,继而求得点B的坐标;
(2)求得直线与x轴的交点,结合B的坐标,观察图象,即可求得使函数值0>y1≥y2的自变量x的取值范围.
解答 解:(1)将点A(1,3)代入反比例函数y2=$\frac{k}{x}$得:3=$\frac{k}{1}$,
解得:k=3,
所以反比例函数表达式为:y2=$\frac{3}{x}$;
将点A代入一次函数y1=x+m得:3=1+m,
解得:m=2,
所以一次函数表达式为:y1=x+2;
将B(-3,n)代入反比例函数y2=$\frac{3}{x}$得:n=$\frac{3}{-3}$=-1,
所以点B的坐标为:(-3,-1).
(2)∵y1=x+2,
令y=0,则0=x+2,x=-2,
∴直线AB与x轴的交点为(-2,0),
∵B(-3,-1),
∴使函数值0>y1≥y2的自变量x的取值范围是-3≤x<-2.
点评 此题考查了反比例函数与一次函数的交点问题、待定系数法求解析式以及不等式和函数的关系.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若关于x的分式方程$\frac{x}{x-2}$-2m=$\frac{3m}{x-2}$无解,则m的值为( )
| A. | m=$\frac{2}{3}$ | B. | m=$\frac{2}{3}$或m=2 | C. | m=$\frac{1}{2}$ | D. | m=$\frac{2}{3}$或m=$\frac{1}{2}$ |
17.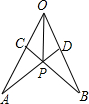 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
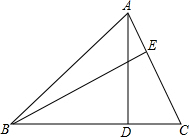 如图,AD,BE分别是△ABC的高,AD=4,BC=6,AC=5,则BE=$\frac{24}{5}$cm.
如图,AD,BE分别是△ABC的高,AD=4,BC=6,AC=5,则BE=$\frac{24}{5}$cm. 已知,∠α
已知,∠α 在△ABC中,D是AB的中点,E是AC的中点,BC=12,则DE=6.
在△ABC中,D是AB的中点,E是AC的中点,BC=12,则DE=6.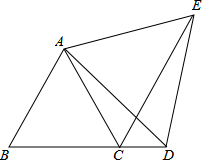 如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.
如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.