题目内容
20.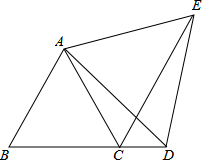 如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.
如图,△ABC为等边三角形,点D在BC的延长线上,CE平分∠ACD,且∠ADE=60°.(1)求证:AC+CD=CE;
(2)求证:△ADE为等边三角形.
分析 (1)作DF∥EC,延长AC交于F,利用等边三角形的性质和全等三角形的判定证明即可;
(2)根据等边三角形的判定解答即可.
解答 证明:(1)作DF∥EC,延长AC交于F,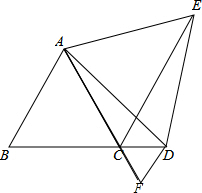
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ACD=120°,
∵CE平分∠ACD,
∴∠ACE=∠ECD=60°,
∵DF∥EC,
∴∠F=∠ACE=60°,∠CDF=∠ECD=60°,
∴△CDF是等边三角形,
∴∠F=60°,CD=CF=DF,
∵∠ACD+∠CDF=∠ACD+∠ADE,
∴∠ADF=∠CDE,
在△FDA与△CDE中,
$\left\{\begin{array}{l}{∠ADF=∠CDE}\\{∠ECD=∠F=60°}\\{CD=DF}\end{array}\right.$,
∴△FDA≌△CDE(AAS),
∴AF=EC,AD=DE,
∴AC+CF=EC,
即AC+CD=EC;
(2)由(1)可知,AD=DE,∠ADE=60°,
故△ADE是等边三角形.
点评 此题考查全等三角形的判定和性质,关键是利用等边三角形的性质和全等三角形的判定证明.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
10.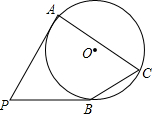 如图,PA,PB是⊙O的切线,切点分别为A,B,∠APB=50°,C是⊙O上一点,则∠ACB的度数为( )
如图,PA,PB是⊙O的切线,切点分别为A,B,∠APB=50°,C是⊙O上一点,则∠ACB的度数为( )
 如图,PA,PB是⊙O的切线,切点分别为A,B,∠APB=50°,C是⊙O上一点,则∠ACB的度数为( )
如图,PA,PB是⊙O的切线,切点分别为A,B,∠APB=50°,C是⊙O上一点,则∠ACB的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
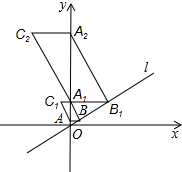 如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B作作直线l的垂线交y轴于点A1,以A1B、AB为邻边作平行四边形A1BAC1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.A1B1为邻边作平行四边形A2B1A1C2;…;则C1的坐标为(-$\sqrt{3}$,4),按此作法继续下去,则Cn的坐标是(-$\sqrt{3}$×4n-1,4n).
如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B作作直线l的垂线交y轴于点A1,以A1B、AB为邻边作平行四边形A1BAC1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.A1B1为邻边作平行四边形A2B1A1C2;…;则C1的坐标为(-$\sqrt{3}$,4),按此作法继续下去,则Cn的坐标是(-$\sqrt{3}$×4n-1,4n). 如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数y2=$\frac{k}{x}$(k为常数,k≠0)的图象相交于点A(1,3)、B(-3,n).
如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数y2=$\frac{k}{x}$(k为常数,k≠0)的图象相交于点A(1,3)、B(-3,n).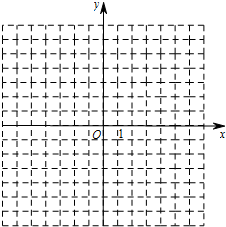
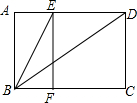 如图所示,已知矩形ABCD与矩形AEFB相似,连接BE,BD,则下列判断中:
如图所示,已知矩形ABCD与矩形AEFB相似,连接BE,BD,则下列判断中: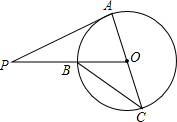 如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,PO交⊙O于点B,若∠P=20°,则∠BCA=35度.
如图,PA是⊙O的切线,A为切点,AC是⊙O的直径,PO交⊙O于点B,若∠P=20°,则∠BCA=35度.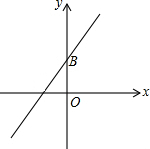 如图,直线y=$\frac{1}{2}$x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=$\frac{1}{2}$x+b上,联结AO,△AOB的面积等于1.
如图,直线y=$\frac{1}{2}$x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=$\frac{1}{2}$x+b上,联结AO,△AOB的面积等于1.