题目内容
3．在平面直角坐标系内点A、B、C、D的坐标分别为（-4，-2）、（-4，1）、（3，3）、（3，-2）．依次连接A、B、C、D（1）请问ABCD是直角梯形（请选择：平行四边形、正方形、直角梯形、等腰梯形）
（2）若点P在图形ABCD内，且△PCD的面积等于△PBC的面积，△PAD的面积：△PAB的面积=7：9．求点P的坐标．
分析 （1）利用网格和点的坐标画图，很容易判断四边形ABCD是等腰梯形；
（2）由△PCD的面积等于△PBC的面积，△PAD的面积：△PAB的面积=7：9．P到AB的距离与到AD的距离的比为3：1，则到CD的距离和到CE的距离相等，即可得到P点坐标．
解答 
解：（1）如图，很容易判断四边形ABCD是直角梯形．
故答案为直角梯形；
（2）P（-1，-1）．
点评 此题主要考查了直角梯形的判定，坐标与图形的性质及三角形的面积等知识点的综合掌握及运用能力．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
13．
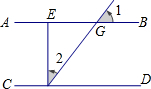如图，若AB∥CD，EF⊥CD，∠1=54°，则∠2为（ ）
如图，若AB∥CD，EF⊥CD，∠1=54°，则∠2为（ ）| A． | 54° | B． | 46° | C． | 44° | D． | 36° |
14．
如图所示，AB∥CD，若∠A=4∠C，则∠A的度数是（ ）
如图所示，AB∥CD，若∠A=4∠C，则∠A的度数是（ ）| A． | 144° | B． | 164° | C． | 126° | D． | 36° |
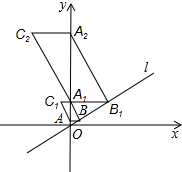如图，在平面直角坐标系中，直线l经过原点，且与y轴正半轴所夹的锐角为60°，过点A（0，1）作y轴的垂线l于点B，过点B作作直线l的垂线交y轴于点A1，以A1B、AB为邻边作平行四边形A1BAC1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2，以A2B1．A1B1为邻边作平行四边形A2B1A1C2；…；则C1的坐标为（-$\sqrt{3}$，4），按此作法继续下去，则Cn的坐标是（-$\sqrt{3}$×4n-1，4n）．
如图，已知一次函数y1=x+m（m为常数）的图象与反比例函数y2=$\frac{k}{x}$（k为常数，k≠0）的图象相交于点A（1，3）、B（-3，n）．
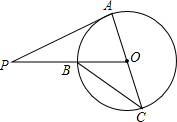如图，PA是⊙O的切线，A为切点，AC是⊙O的直径，PO交⊙O于点B，若∠P=20°，则∠BCA=35度．
如图，在Rt△ABC中，∠C=90°，∠A=30°，AC=8，求斜边AB的长．