题目内容
20.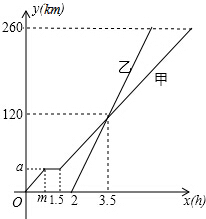 甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:①m=1,a=40;
②甲车的速度是40千米/小时,乙车的速度是80千米/小时;
③当甲车距离A地260千米时,甲车所用的时间为7小时;
④当两车相距20千米时,则乙车行驶了3或4小时,
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①观察图象找出点(3.5,120),根据“速度=路程÷行驶时间”可以算出甲车的速度,再结合甲车中途休息半个小时即可得出a、m的值;
②根据点(3.5,120),利用“速度=路程÷行驶时间”可以算出乙车的速度;
③根据“时间=路程÷速度”可算出甲车距离A地260千米时行驶的时间,加上休息的0.5小时即可得出结论;
④根据点(3.5,120),结合两车速度差即可算出当两车相距20千米时,甲车行驶的时间,再根据甲车比乙车早出发2小时可得出乙车行驶时间.
对比给定的说法即可得出结论.
解答 解:①∵甲车途中休息了0.5小时,
∴m=1.5-0.5=1,
甲车的速度为:120÷(3.5-0.5)=40(千米/小时).
a=1×40=40.
∴①成立;
②乙车的速度为:120÷(3.5-2)=80(千米/时),
∴甲车的速度是40千米/小时,乙车的速度是80千米/小时,②成立;
③当甲车距离A地260千米时,甲车所用的时间为:260÷40+0.5=7(小时),
∴③成立;
④∵两车相遇时时间为3.5时,且甲车速度为40千米/时,乙车速度为80千米/时,
∴当两车相距20千米时,甲车行驶的时间为:3.5+20÷(80-40)=4(小时)或3.5-20÷(80-40)=3(小时),
又∵甲车比乙车早出发2小时,
∴当两车相距20千米时,则乙车行驶了1或2小时,④不正确.
综上可知:正确的结论有①②③.
故选C.
点评 本题考查了一次函数的应用,解题的关键是结合图形找出点的坐标.本题属于基础题,难度不大,解决该题型题目时,观察图形找出点的坐标,再根据各数量之间的关系即可求出结论.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
17.某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数为6,10,5,3,4,8,4,这组数据的众数和极差分别是( )
| A. | 5,7 | B. | 7,5 | C. | 4,7 | D. | 3,7 |
5. 如图,△ABC中,∠BAC=70°,将△ABC绕点C顺时针旋转一定角度,得到△DEC,点A的对应点为D,ED过点A,则旋转角的度数为( )
如图,△ABC中,∠BAC=70°,将△ABC绕点C顺时针旋转一定角度,得到△DEC,点A的对应点为D,ED过点A,则旋转角的度数为( )
 如图,△ABC中,∠BAC=70°,将△ABC绕点C顺时针旋转一定角度,得到△DEC,点A的对应点为D,ED过点A,则旋转角的度数为( )
如图,△ABC中,∠BAC=70°,将△ABC绕点C顺时针旋转一定角度,得到△DEC,点A的对应点为D,ED过点A,则旋转角的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
 在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.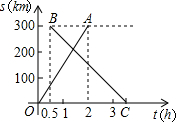 在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题:
在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题: