题目内容
9.先化简,再求值:(1+$\frac{1}{x-2}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-4}$,其中x是不等式组$\left\{\begin{array}{l}{-x-2≤3}\\{2x<12}\end{array}\right.$的最大正整数解.分析 先算括号里面的加法,再算除法,再求出不能等式的解集,在此解集范围内找出符合条件的x的值代入进行计算即可.
解答 解:原式=$\frac{x-1}{x-2}$•$\frac{(x+2)(x-2)}{(x-1)^{2}}$
=$\frac{x+2}{x-1}$,
解不等式组$\left\{\begin{array}{l}{-x-2≤3}\\{2x<12}\end{array}\right.$得,-5≤x<6,
∵x是不能等式组的最大整数解,
∴x=5,
∴原式=$\frac{5+2}{5-1}$=$\frac{7}{4}$.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
相关题目
17.下列二次根式中,不能与$\sqrt{3}$合并的是( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{27}$ |
14.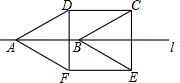 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为( )
 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折得到四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
1.如果a与b互为相反数,那么a+b=( )
| A. | -2a | B. | 0 | ||
| C. | 2a | D. | 以上答案均不正确 |
19.据大连市公安局统计,2016年全市约有410000人换二代居民身份证,将410000用科学记数法表示应为( )
| A. | 0.41×104 | B. | 41×104 | C. | 4.1×106 | D. | 4.1×105 |
 如图,PA是⊙O的切线,切点为A,PA=$\sqrt{3}$,∠APO=30°,则⊙O的半径为1.
如图,PA是⊙O的切线,切点为A,PA=$\sqrt{3}$,∠APO=30°,则⊙O的半径为1.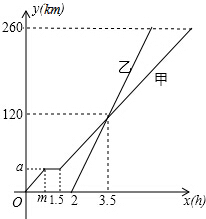 甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法:
甲、乙两车从A地匀速驶向B地,甲车比乙车早出发2小时,并且甲车图中休息了0.5小时后仍以原速度驶向B地,如图是甲、乙两车行驶的路程y(千米)与行驶的时间x(小时)之间的函数图象.下列说法: 如图,已知菱形ABCD中,AC=6cm,BD=8cm,则菱形的高AE为$\frac{24}{5}$cm.
如图,已知菱形ABCD中,AC=6cm,BD=8cm,则菱形的高AE为$\frac{24}{5}$cm.