题目内容
4.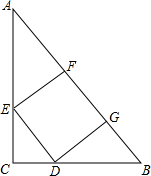 如图所示,Rt△ABC中,AC=4,BC=3,正方形DEFG的顶点分别在Rt△ABC的边上,则正方形的边长为$\frac{60}{37}$.
如图所示,Rt△ABC中,AC=4,BC=3,正方形DEFG的顶点分别在Rt△ABC的边上,则正方形的边长为$\frac{60}{37}$.
分析 过C作CH⊥AB与H,交DE于P,根据正方形的性质得到DE∥GF,DG=EF=FG=DE,根据相似三角形的性质列方程,即可得到结论.
解答  解:过C作CH⊥AB与H,交DE于P,
解:过C作CH⊥AB与H,交DE于P,
∵四边形DGFE是正方形,
∴DE∥GF,DG=EF=FG=DE,
∴CP⊥DE,
∵Rt△ABC中,AC=4,BC=3,
∴AB=5,CH=$\frac{12}{5}$,
∵DE∥AB,
∴△CDE∽△CBA,
∴$\frac{DE}{AB}=\frac{CP}{CH}$,
设正方形的边长是x,
∴$\frac{x}{5}=\frac{\frac{12}{5}-x}{\frac{12}{5}}$,
∴x=$\frac{60}{37}$,
∴正方形的边长为$\frac{60}{37}$,
故答案为:$\frac{60}{37}$.
点评 本题考查了相似三角形的判定与性质以及正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 圆锥的母线与高的夹角为30°,母线长为6cm,求它的侧面积.
圆锥的母线与高的夹角为30°,母线长为6cm,求它的侧面积. 已知:两条定直线a,b在直线a上有一个定点A,在直线a上求一点B,在直线b上求一点P,使两点A、B与点P的连线总长最短.
已知:两条定直线a,b在直线a上有一个定点A,在直线a上求一点B,在直线b上求一点P,使两点A、B与点P的连线总长最短.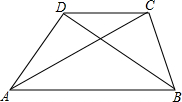 如图,已知梯形ABCD中,AB∥CD,AD>BC.求证:AC>BD.
如图,已知梯形ABCD中,AB∥CD,AD>BC.求证:AC>BD. 如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.
如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值. 如图,一位牧童每天都要从A地出发赶着牛到河边饮水,然后再到B地放牧,应该怎样选择饮水的地点,才能使牛所走的路线最短?
如图,一位牧童每天都要从A地出发赶着牛到河边饮水,然后再到B地放牧,应该怎样选择饮水的地点,才能使牛所走的路线最短?