题目内容
19.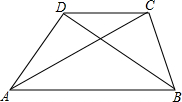 如图,已知梯形ABCD中,AB∥CD,AD>BC.求证:AC>BD.
如图,已知梯形ABCD中,AB∥CD,AD>BC.求证:AC>BD.
分析 过D作DF⊥AB于F,过C作CE⊥AB于E,得出四边形DFEC是矩形,根据矩形的性质得出DC=EF,DF=CE,由勾股定理得出AF>BE,由勾股定理求出AC2>BD2,即可得出答案.
解答 证明: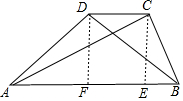
过D作DF⊥AB于F,过C作CE⊥AB于E,
则DF∥EC,∠DFE=90°,
∵DC∥AB,
∴四边形DFEC是矩形,
∴DC=EF,DF=CE,
∵AD>BC,
∴在Rt△AFD和Rt△CEB中,由勾股定理得出AF>BE,
∴AE>BF,
由勾股定理得:AC2=CE2+AE2,BD2=DF2+BF2,
∴AC2>BD2,
∴AC>BD.
点评 本题考查了勾股定理,梯形的性质,矩形的性质和判定的应用,能正确作出辅助线是解此题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
3.(-2)2的平方根是( )
| A. | ±2 | B. | -2 | C. | 2 | D. | $\sqrt{2}$ |
7.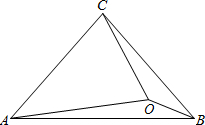 △ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )
△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )
 △ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )
△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )| A. | 55° | B. | 60° | C. | 70° | D. | 80° |
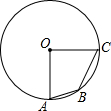 如图,已知A,B,C均在圆O上,且OA⊥OC,AB=1,BC=$\sqrt{2}$,则OABC的面积为$\frac{7}{4}$.
如图,已知A,B,C均在圆O上,且OA⊥OC,AB=1,BC=$\sqrt{2}$,则OABC的面积为$\frac{7}{4}$.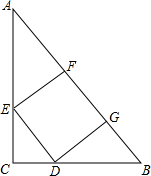 如图所示,Rt△ABC中,AC=4,BC=3,正方形DEFG的顶点分别在Rt△ABC的边上,则正方形的边长为$\frac{60}{37}$.
如图所示,Rt△ABC中,AC=4,BC=3,正方形DEFG的顶点分别在Rt△ABC的边上,则正方形的边长为$\frac{60}{37}$.
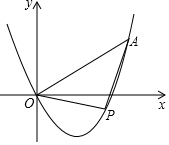 如图,二次函数y=ax2-(4a-0.5)x(a>0)的图象经过点A(4,m),若点P是这个二次函数图象上的一个动点,当△POA为等腰直角三角形时,a的值是$\frac{5}{6}$或$\frac{5}{4}$或$\frac{5}{12}$.
如图,二次函数y=ax2-(4a-0.5)x(a>0)的图象经过点A(4,m),若点P是这个二次函数图象上的一个动点,当△POA为等腰直角三角形时,a的值是$\frac{5}{6}$或$\frac{5}{4}$或$\frac{5}{12}$.