题目内容
9. 如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.
如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.
分析 作OH⊥CD于H,OF交CD于G,连接CE,如图,利用点O为矩形ABCD的对角线AC的中点得到OH=$\frac{1}{2}$BC=1,CH=2,利用等角的余角相等得到∠1=∠2,再利用切线的性质得CE⊥OE,所以OF∥CE,则∠1=∠3=∠2,接着证明△CEG≌△OHG得到EG=HG,设EG=x,则HG=x,CG=2-x,利用勾股定理得到12+x2=(2-x)2,解得x=$\frac{3}{4}$,然后在Rt△CEG中利用正切定义得到tan∠3=$\frac{3}{4}$,从而得到tan∠OFC的值.
解答 解:作OH⊥CD于H,OF交CD于G,连接CE,如图,
∵点O为矩形ABCD的对角线AC的中点,
∴OH=$\frac{1}{2}$BC=1,CH=$\frac{1}{2}$CD=2,
∵OF⊥OE,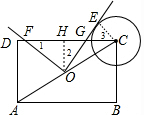
∴∠FOG=90°,即∠FOH+∠2=90°,
而∠FOH+∠1=90°,
∴∠1=∠2,
∵OE为切线,
∴CE⊥OE,
∴OF∥CE,
∴∠1=∠3,
∴∠2=∠3,
在△CEG和△OHG中
$\left\{\begin{array}{l}{∠CGE=∠OGH}\\{∠3=∠2}\\{CE=OH}\end{array}\right.$,
∴△CEG≌△OHG,
∴EG=HG,
设EG=x,则HG=x,CG=2-x,
在Rt△CEG中,12+x2=(2-x)2,解得x=$\frac{3}{4}$,
在Rt△CEG中,tan∠3=$\frac{EG}{CE}$=$\frac{3}{4}$,
∴tan∠OFC的值为$\frac{3}{4}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了矩形的性质和三角形全等的判定与性质.

| A. | △>M | B. | △=M | ||
| C. | △<M | D. | 无法确定△与M的大小 |
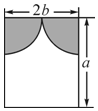 长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )
长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是( )| A. | 2a2-πb2 | B. | 2a2-$\frac{π}{2}$b2 | C. | 2ab-πb2 | D. | 2ab-$\frac{π}{2}$b2 |
 用一个圆心角为120°、半径为18cm的扇形作一个圆锥的侧面.求圆锥底面积圆的半径R.
用一个圆心角为120°、半径为18cm的扇形作一个圆锥的侧面.求圆锥底面积圆的半径R. 张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案:
张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:米,卫生间的宽未定,设宽为x米),售房部为张先生提供了以下两种优惠方案: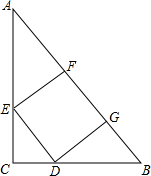 如图所示,Rt△ABC中,AC=4,BC=3,正方形DEFG的顶点分别在Rt△ABC的边上,则正方形的边长为$\frac{60}{37}$.
如图所示,Rt△ABC中,AC=4,BC=3,正方形DEFG的顶点分别在Rt△ABC的边上,则正方形的边长为$\frac{60}{37}$.