题目内容
12.若a、b、c、d均为正实数,已知下列四个方程:(1)$\frac{1}{2}$x2+$\sqrt{2a+b}$x+$\sqrt{cd}$=0;
(2)$\frac{1}{2}$x2+$\sqrt{2b+c}$x+$\sqrt{ad}$=0;
(3)$\frac{1}{2}$x2+$\sqrt{2c+d}$x+$\sqrt{ab}$=0;
(4)$\frac{1}{2}$x2+$\sqrt{2d+a}$x+$\sqrt{bc}$=0
试说明:这四个方程中至少有两个方程有不相等的实数根.
分析 利用反证法,假设假设这四个方程中最多只有一个方程有不相等的实数根,令方程(1)有两个不等的实数根,结合根的判别式可得出“①2b+c≤2$\sqrt{ad}$;②2c+a≤2$\sqrt{ab}$;③2d+a≤2$\sqrt{bc}$”,将三个不等式相加结合“若m、n为正实数,则m+n≥2$\sqrt{mn}$”可得出2c+d≤0,这与a、b、c、d均为正实数冲突,由此得出假设不成立,从而证出结论.
解答 证明:假设这四个方程中最多只有一个方程有不相等的实数根,
不失一般性,令方程(1)有两个不相等的实数根,
则由根的判别式可知:
①2b+c≤2$\sqrt{ad}$;②2c+a≤2$\sqrt{ab}$;③2d+a≤2$\sqrt{bc}$.
①+②+③可知:
2a+2b+3c+2d≤2($\sqrt{ad}$+$\sqrt{ab}$+$\sqrt{bc}$)≤a+d+a+b+b+c=2a+2b+c+d,
∴2c+d≤0.
∵a、b、c、d均为正实数,
∴结论不成立.
故这四个方程中至少有两个方程有不相等的实数根.
点评 本题考查了反证法的应用、根的判别式,解题的关键是利用反证法证出“这四个方程中最多只有一个方程有不相等的实数根”不成立.本题属于基础题,难度不大,解决该题型题目时,首先要想到利用反证法,找出结论的反命题,通过根的判别式得出假设不成立,从而证出原结论成立.

练习册系列答案
相关题目
17.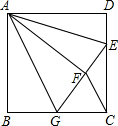 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
①点G是BC的中点;
②FG=FC;
③AG∥CF;
④S△FGC=$\frac{9}{10}$.
其中正确结论是( )
 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC的中点;
②FG=FC;
③AG∥CF;
④S△FGC=$\frac{9}{10}$.
其中正确结论是( )
| A. | ①② | B. | ②④ | C. | ①②③ | D. | ①③④ |
13.下列说法中正确的个数有( )
①正方体的所有棱长都相等
②圆锥的侧面展开图是扇形
③圆柱的侧面是长方形.
①正方体的所有棱长都相等
②圆锥的侧面展开图是扇形
③圆柱的侧面是长方形.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
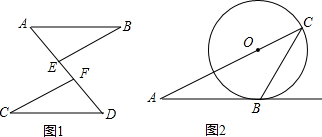
 如图,在△ABC中,已知AB=AC=5,BC=6,点D、E分别在BC、AC上,且∠ADE=∠B
如图,在△ABC中,已知AB=AC=5,BC=6,点D、E分别在BC、AC上,且∠ADE=∠B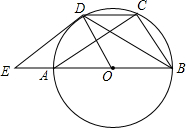 如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB
如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB