题目内容
13. 如图所示,Rt△ABC中,∠ACB=90°,点A坐标为(0,1),点B坐标为(0,-1),且∠ABC=30°,若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,则k的值为$\frac{\sqrt{3}}{4}$.
如图所示,Rt△ABC中,∠ACB=90°,点A坐标为(0,1),点B坐标为(0,-1),且∠ABC=30°,若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,则k的值为$\frac{\sqrt{3}}{4}$.
分析 过点C作CD⊥y轴于点D,由点A(0,1)、点B(0,-1)结合解直角三角形可得出点C的坐标,再由点C的坐标结合反比例函数图象上点的坐标特征可得出结论.
解答 解:过点C作CD⊥y轴于点D,如图所示.
在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=1-(-1)=2,
∴AC=AB•sin∠ABC=2×$\frac{1}{2}$=1,
CD=AC•cos∠ABC=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,AD=AC•sin∠ABC=1×$\frac{1}{2}$=$\frac{1}{2}$,
∴点C的坐标为(1-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
∴k=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题考查了反比例函数图象上点的坐标特征以及解直角三角形,解题的关键是找出点C的坐标.本题属于基础题,难度不大,解决该题型题目时,通过解直角三角形找出点的坐标,再结合反比例函数图象上点的坐标特征即可得以解决.

练习册系列答案
相关题目
13.下列说法中正确的个数有( )
①正方体的所有棱长都相等
②圆锥的侧面展开图是扇形
③圆柱的侧面是长方形.
①正方体的所有棱长都相等
②圆锥的侧面展开图是扇形
③圆柱的侧面是长方形.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
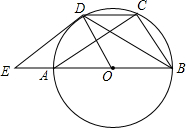 如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB
如图,⊙O是△ABC的外接圆,AB是直径,点D是$\widehat{AC}$的中点,E为BA延长线上一点,且∠DEB=∠CDB