题目内容
18.生活中人们常把信纸按着下图的顺序进行折叠(阴影部分表示纸条反面)(l)如果信纸折成的长方形纸条宽为2cm,为了保证能折成图④形状(即纸条两端均刚好到达点P),纸条长至少多少厘米?
(2)折叠后得到的四边形MNEF是什么四边形?并说明理由.
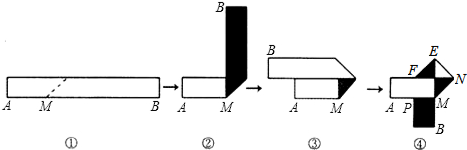
分析 (1)根据折叠的性质知,纸条长至少是宽的5倍,进一步求得纸条长和面积即可;
(2)四边形MNEF是正方形,根据正方形定义只要证明四边形MNEF是平行四边形,邻边相等,有一个角是直角即可.
解答 解:(1)设纸条为xcm,由折纸过程可知:x≥5×2即x≥10,
∴纸条长至少10厘米.
(2)四边形MNEF是正方形,
理由:由折纸过程可知,∠EMN=∠MEN=45°,
∴EN=MN,∠MNE=90°,同理EF=EN,∠FEN=90°,
∴∠MNE+∠FEN=180°,
∴EF∥MN,∵EF=MN,
∴四边形MNEF是平行四边形,
∵MN=NE,
∴四边形MNEF是菱形,
∵∠MNE=90°,
∴四边形MNEF是正方形.
点评 此题考查了翻折变换,折叠的性质,注意掌握数形结合思想的应用.实际动手操作,更能够清楚地发现中间的长度和宽之间的关系,难点是发现纸条长至少是宽的5倍.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB∥CD,EF交AB于点E,交CD于点F,FG,EG分别平分∠CFE和∠AEF,FH,EH分别平分∠DFE和∠BEF,求证:四边形EGFH是矩形.
如图,AB∥CD,EF交AB于点E,交CD于点F,FG,EG分别平分∠CFE和∠AEF,FH,EH分别平分∠DFE和∠BEF,求证:四边形EGFH是矩形. 已知如图,正方形ABCD的边长为1,P是CD边的中点,点Q在线段BC上,设BQ=k,是否存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似?若存在,求出k的值;若不存在,请说明理由.
已知如图,正方形ABCD的边长为1,P是CD边的中点,点Q在线段BC上,设BQ=k,是否存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似?若存在,求出k的值;若不存在,请说明理由. 如图.在△ABC中,点D在BC边上,BD=DC,点E在AD上,CF∥AB,∠BAD=∠DEF,若AB=5,CF=2.则线段EF的长为3.
如图.在△ABC中,点D在BC边上,BD=DC,点E在AD上,CF∥AB,∠BAD=∠DEF,若AB=5,CF=2.则线段EF的长为3.