题目内容
8．如图是用正三角形、正方形、正六边形设计的一组图案，按照如下规律，第n个图案中正三角形的个数是4n+2．
分析 分析可知规律是每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个．
解答 解：∵第一个图案正三角形个数为6=2+4；
第二个图案正三角形个数为2+4+4=2+2×4；
第三个图案正三角形个数为2+2×4+4=2+3×4；
…
∴第n个图案正三角形个数为2+（n-1）×4+4=2+4n=4n+2．
故答案为：4n+2．
点评 此题考查了平面图形，主要培养学生的观察能力和空间想象能力，根据已知图形发现变化与不变的部分及变化部分按照何种规律变化是关键．
练习册系列答案
相关题目
19．若3x2n-1ym与-5xmy3是同类项，则m，n的值分别是（ ）
| A． | 3，-2 | B． | -3，2 | C． | 3，2 | D． | -3，-2 |
13．
如图，直线a∥b，直线c是截线，如果∠1=65°，那么∠2等于（ ）
如图，直线a∥b，直线c是截线，如果∠1=65°，那么∠2等于（ ）| A． | 165° | B． | 135° | C． | 125° | D． | 115° |
20．若点P（3k-1，1-k）在第四象限，则k的取值范围为（ ）
| A． | k＞1 | B． | k＞$\frac{1}{3}$ | C． | $\frac{1}{3}$＜k＜1 | D． | k＜$\frac{1}{3}$ |
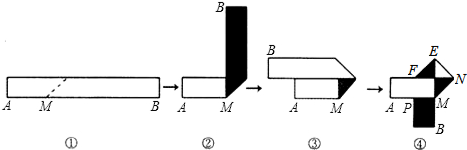
如图，将一个长方形的铁皮剪取一小块的长方形铁皮：