题目内容
16.有序数对(m,n)中的整数m,n满足m-n=-6,且点P(m,n)在第二象限,写出所有符合条件的数对.分析 根据第二象限内点的坐标特征得$\left\{\begin{array}{l}{m<0}\\{n>0}\end{array}\right.$,而m-n=-6,则$\left\{\begin{array}{l}{n-6<0}\\{n>0}\end{array}\right.$,解得0<n<6,所以整数n=1,2,3,4,5共5个值,则对应地m有5个值,所以P点共有5个.
解答 解:∵P在第二象限,
∴$\left\{\begin{array}{l}{m<0}\\{n>0}\end{array}\right.$,而m-n=-6,
∴$\left\{\begin{array}{l}{n-6<0}\\{n>0}\end{array}\right.$,解得0<n<6,
∴整数n=1,2,3,4,5,共5个值,
对应地m有5个值,m=-5,-4,-3,-2,-1,
所以P点共有5个,即(-5,1),(-4,2),(-3,3),(-2,4),(-1,5).
点评 本题考查了点的坐标:我们把有顺序的两个数a和b组成的数对,叫做有序数对,记作(a,b);记住坐标轴上点的坐标特征和各象限内点的坐标特征.也考查了非负数性质.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
6.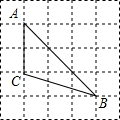 如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
 如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
19.若3x2n-1ym与-5xmy3是同类项,则m,n的值分别是( )
| A. | 3,-2 | B. | -3,2 | C. | 3,2 | D. | -3,-2 |
 如图,已知点A是⊙O上一点,直线MN过点A,点B是MN上的另一点,点C是OB的中点,AC=$\frac{1}{2}$OB,若点P是⊙O上的一个动点,且∠OBA=30°,AB=$2\sqrt{3}$时,求△APC的面积的最大值.
如图,已知点A是⊙O上一点,直线MN过点A,点B是MN上的另一点,点C是OB的中点,AC=$\frac{1}{2}$OB,若点P是⊙O上的一个动点,且∠OBA=30°,AB=$2\sqrt{3}$时,求△APC的面积的最大值.