题目内容
13.已知点P为等边△ABC内一点,∠APB=112°,∠APC=122°,若以AP、BP、CP为边长可以构成一个三角形,那么所构成三角形的各内角的度数是52°、62°、66°.分析 如图,将△APC绕点A顺时针旋转60°得到△ABE,连接PE,只要证明PA、PB、PC为边组成的三角形就是△PEB,再求出其内角即可.
解答 解:如图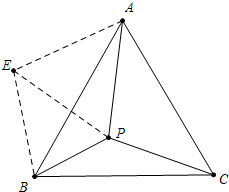 ,将△APC绕点A顺时针旋转60°得到△ABE,连接PE.
,将△APC绕点A顺时针旋转60°得到△ABE,连接PE.
∵AE=AP,∠EAP=∠BAC=60°,
∴△EAP是等边三角形,∠EAB=∠PAC,
∴∠AEP=∠APE=60°,PA=PE,
在△EAP和△PAC中,
$\left\{\begin{array}{l}{EA=AP}\\{∠EAP=∠PAC}\\{AB=AC}\end{array}\right.$,
∴△EAP≌△PAC,
∴EB=PC,
∴PA、PB、PC组成的三角形就是△PEB,
∵∠APB=112°,∠APE=60°,
∴∠EPB=52,
∵∠AEB=∠APC=122°,∠AEP=62°,
∴∠PEB=66°,
∴∠EBP=180°-∠BEP-∠EPB=66°.
故答案为52°、62°、66°.
点评 本题考查等边三角形的性质、旋转的性质,利用旋转添加辅助线是解决问题的关键,属于中考常考题型.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图,已知点A是⊙O上一点,直线MN过点A,点B是MN上的另一点,点C是OB的中点,AC=$\frac{1}{2}$OB,若点P是⊙O上的一个动点,且∠OBA=30°,AB=$2\sqrt{3}$时,求△APC的面积的最大值.
如图,已知点A是⊙O上一点,直线MN过点A,点B是MN上的另一点,点C是OB的中点,AC=$\frac{1}{2}$OB,若点P是⊙O上的一个动点,且∠OBA=30°,AB=$2\sqrt{3}$时,求△APC的面积的最大值.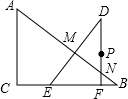 如图,在Rt△ABC张,∠C=90°,AC=9cm,BC=12cm,在Rt△DEF中,∠DFE=90°,EF=6cm,DF=8cm.点C,B,E,F在同一直线上,且B,F重合.现固定△ABC不动,将Rt△DEF沿直线BC以1cm/s的速度向点C平移,同时点P从点F出发,以2cm/s的速度向点D运动.设DE,DF两边分别于AB边交于M,N两点,在运动过程中,当PM=PN时,t的值为$\frac{32}{13}$.
如图,在Rt△ABC张,∠C=90°,AC=9cm,BC=12cm,在Rt△DEF中,∠DFE=90°,EF=6cm,DF=8cm.点C,B,E,F在同一直线上,且B,F重合.现固定△ABC不动,将Rt△DEF沿直线BC以1cm/s的速度向点C平移,同时点P从点F出发,以2cm/s的速度向点D运动.设DE,DF两边分别于AB边交于M,N两点,在运动过程中,当PM=PN时,t的值为$\frac{32}{13}$.
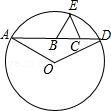 如图,A、B、C、D依次为一直线上4个点,BC=4,△BCE为等边三角形,⊙O过A、D、E三点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为y=$\frac{16}{x}$.
如图,A、B、C、D依次为一直线上4个点,BC=4,△BCE为等边三角形,⊙O过A、D、E三点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为y=$\frac{16}{x}$.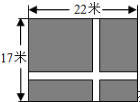 如图,在一块长为22m,宽为17m的矩形地面内,要修筑两条同样宽且互相垂直的道路(两条道路分别与矩形的一条边平行),余下的铺上草坪,要使草坪的面积达到300m2.设道路的宽为x m,根据题意列方程(20-x)(32-x)=300.
如图,在一块长为22m,宽为17m的矩形地面内,要修筑两条同样宽且互相垂直的道路(两条道路分别与矩形的一条边平行),余下的铺上草坪,要使草坪的面积达到300m2.设道路的宽为x m,根据题意列方程(20-x)(32-x)=300.