题目内容
6.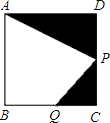 已知如图,正方形ABCD的边长为1,P是CD边的中点,点Q在线段BC上,设BQ=k,是否存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似?若存在,求出k的值;若不存在,请说明理由.
已知如图,正方形ABCD的边长为1,P是CD边的中点,点Q在线段BC上,设BQ=k,是否存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似?若存在,求出k的值;若不存在,请说明理由.
分析 存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似,要分两种情况①点Q与点B重合时的情况;②点Q与点B不重合时,由△ADP∽△PCQ相似的性质,可得AD:DP=PC:CQ,分别讨论解答.
解答 解:存在这样的实数k,使得Q、C、P为顶点的三角形与△ADP相似,理由如下:
根据题意,当Q点与B重合时,△ADP≌△PCQ,此时k=0;
当△ADP∽△PCQ时,AD:DP=PC:CQ,
∵正方形ABCD的边长为1,P是CD边的中点,
∴AD=1,PD=0.5,PC=0.5,CQ=1-k,
即1:0.5=0.5(1-k),解得k=0.75.
综上可知:k=0或0.75.
点评 本题考查了正方形的四条边都相等的性质,相似三角形的对应边成比例的性质,因为对应边不明确,所以要分情况讨论求解,避免漏解而导致出错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.一列单项式按以下规律排列:x,3x2,5x2,7x,9x2,l1x2,13x,…,则第2015个单项式应是( )
| A. | 4029x | B. | 4029x2 | C. | 4027x | D. | 4027x2 |
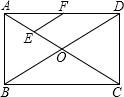 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=12cm,BD=16cm,则△AEF的周长为15cm.
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=12cm,BD=16cm,则△AEF的周长为15cm. 如图,已知点A是⊙O上一点,直线MN过点A,点B是MN上的另一点,点C是OB的中点,AC=$\frac{1}{2}$OB,若点P是⊙O上的一个动点,且∠OBA=30°,AB=$2\sqrt{3}$时,求△APC的面积的最大值.
如图,已知点A是⊙O上一点,直线MN过点A,点B是MN上的另一点,点C是OB的中点,AC=$\frac{1}{2}$OB,若点P是⊙O上的一个动点,且∠OBA=30°,AB=$2\sqrt{3}$时,求△APC的面积的最大值.