题目内容
3. 如图.在△ABC中,点D在BC边上,BD=DC,点E在AD上,CF∥AB,∠BAD=∠DEF,若AB=5,CF=2.则线段EF的长为3.
如图.在△ABC中,点D在BC边上,BD=DC,点E在AD上,CF∥AB,∠BAD=∠DEF,若AB=5,CF=2.则线段EF的长为3.
分析 延长AD,CF交于G,通过△ABD≌△CDG,得到AB=CG,∠BAD=∠G,等量代换得到∠DEF=∠G,由等腰三角形的性质得到EF=FG,等量代换即可得到结论.
解答  解:延长AD,CF交于G,
解:延长AD,CF交于G,
∵CF∥AB,
∴∠B=∠BCF,
在△ABD与△GCD中,$\left\{\begin{array}{l}{∠B=∠BCF}\\{BD=CD}\\{∠ADB=∠CDG}\end{array}\right.$,
∴△ABD≌△CDG,
∴AB=CG,∠BAD=∠G,
∵∠BAD=∠DEF,
∴∠DEF=∠G,
∴EF=FG,
∵AB=5,CF=2,
∴CG=5,
∴EF=FG=5-2=3.
故答案为:3.
点评 本题考查了全等三角形的判定和性质,等腰三角形的判定和性质,平行线的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
15.一列单项式按以下规律排列:x,3x2,5x2,7x,9x2,l1x2,13x,…,则第2015个单项式应是( )
| A. | 4029x | B. | 4029x2 | C. | 4027x | D. | 4027x2 |
12.做大小两个纸盒,尺规如下(单位:cm)
(1)做这两个纸盒共用料多少平方厘米?(结果用含a、b、c的代数式表示)
(2)做成的大纸盒比小纸盒的容积大多少立方厘米?(结果用含a、b、c的代数式表示)
| 长 | 宽 | 高 | |
| 小纸盒 | a | b | c |
| 大纸盒 | 3a | 2b | 2c |
(2)做成的大纸盒比小纸盒的容积大多少立方厘米?(结果用含a、b、c的代数式表示)
13. 如图,直线a∥b,直线c是截线,如果∠1=65°,那么∠2等于( )
如图,直线a∥b,直线c是截线,如果∠1=65°,那么∠2等于( )
 如图,直线a∥b,直线c是截线,如果∠1=65°,那么∠2等于( )
如图,直线a∥b,直线c是截线,如果∠1=65°,那么∠2等于( )| A. | 165° | B. | 135° | C. | 125° | D. | 115° |
 如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.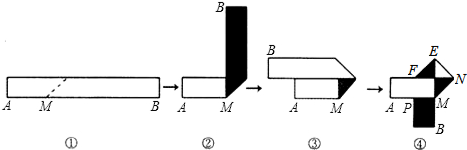
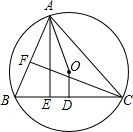 如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).
如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).