题目内容
15. 如图,AB∥CD,EF交AB于点E,交CD于点F,FG,EG分别平分∠CFE和∠AEF,FH,EH分别平分∠DFE和∠BEF,求证:四边形EGFH是矩形.
如图,AB∥CD,EF交AB于点E,交CD于点F,FG,EG分别平分∠CFE和∠AEF,FH,EH分别平分∠DFE和∠BEF,求证:四边形EGFH是矩形.
分析 根据平行线的性质可得∠AEF+∠CFE=180°,再根据角平分线的性质可得∠1=$\frac{1}{2}$∠AEF,∠2=$\frac{1}{2}$∠CFE,然后可证明∠G=90°,同理可得∠H=90°,再证明∠2+∠EFD=90°,可根据三个角是直角的四边形是矩形.
解答 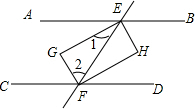 证明:∵AB∥CD,
证明:∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵EG分别平分∠CFE和∠AEF,
∴∠1=$\frac{1}{2}$∠AEF,∠2=$\frac{1}{2}$∠CFE,
∴∠1+∠2=90°,
∴∠G=90°,
同理可得∠H=90°,
∵FH平分∠EFD,
∴∠EFH=$\frac{1}{2}$∠EFD,
∴∠2+∠EFD=$\frac{1}{2}$∠CFE+$\frac{1}{2}$∠EFD=90°,
∴四边形EGFH是矩形.
点评 此题主要考查了矩形的判定,关键是掌握矩形的判定定理:①矩形的定义:有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形(或“对角线互相平分且相等的四边形是矩形”).

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
6.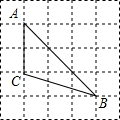 如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
 如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )
如图,方格中的每个小正方形的边长均为1,已知△ABC的三个顶点均在小正方形的顶点上,则sinB的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
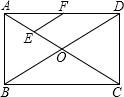 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=12cm,BD=16cm,则△AEF的周长为15cm.
如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=12cm,BD=16cm,则△AEF的周长为15cm. 如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.