题目内容
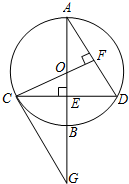 如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,
如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,连接CO并延长交AD于点F,且CF⊥AD.
(1)试问:CG是⊙O的切线吗?说明理由;
(2)求证:E为OB的中点;
(3)若AB=8,求弧BC、CG、BG组成的图形的面积.
考点:切线的判定,扇形面积的计算
专题:
分析:(1)根据平行线的性质求出OC⊥CG,根据切线的判定得出即可;
(2)根据垂径定理求出CE=DE,证△BDE∽△OCE,得出比例式,即可得出OE=BE,即可得出答案;
(3)求出OC和OE,即可求出∠COE和∠G,分别求出△OCG和扇形COB的面积,即可求出答案.
(2)根据垂径定理求出CE=DE,证△BDE∽△OCE,得出比例式,即可得出OE=BE,即可得出答案;
(3)求出OC和OE,即可求出∠COE和∠G,分别求出△OCG和扇形COB的面积,即可求出答案.
解答:(1)解:CG是⊙O的切线,
理由是:∵CG∥AD,
∴∠FCG+∠CFD=180°,
∵CF⊥AD,
∴∠CFG=90°,
∴∠FCG=90°,
即OC⊥CG,
∴CG是⊙O的切线;
(2)证明: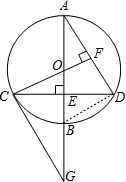 连接BD,
连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠AFO=90°,
∴DB∥CF,
∴△BDE∽△OCE,
∴
=
,
∵AE⊥CD,且AE过圆心O,
∴CE=DE,
∴BE=OE,
即点E为OB的中点;
(3)解: ∵直径AB=8,
∵直径AB=8,
∴OC=4,OB=4,OE=2,
∴∠OCE=30°,
∵∠OEC=90°,
∴∠COE=60°,
∵∠OCG=90°,
∴∠G=90°-60°=30°,
∴OG=2OC=8,由勾股定理得:CG=
=4
,
∴弧BC、CG、BG组成的图形的面积S=S△OCG-S扇形COB=
×4×4
-
=8
-
π.
理由是:∵CG∥AD,
∴∠FCG+∠CFD=180°,
∵CF⊥AD,
∴∠CFG=90°,
∴∠FCG=90°,
即OC⊥CG,
∴CG是⊙O的切线;
(2)证明:
 连接BD,
连接BD,∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠AFO=90°,
∴DB∥CF,
∴△BDE∽△OCE,
∴
| BE |
| OE |
| DE |
| CE |
∵AE⊥CD,且AE过圆心O,
∴CE=DE,
∴BE=OE,
即点E为OB的中点;
(3)解:
 ∵直径AB=8,
∵直径AB=8,∴OC=4,OB=4,OE=2,
∴∠OCE=30°,
∵∠OEC=90°,
∴∠COE=60°,
∵∠OCG=90°,
∴∠G=90°-60°=30°,
∴OG=2OC=8,由勾股定理得:CG=
| 82-42 |
| 3 |
∴弧BC、CG、BG组成的图形的面积S=S△OCG-S扇形COB=
| 1 |
| 2 |
| 3 |
| 60π•42 |
| 360 |
| 3 |
| 8 |
| 3 |
点评:本题考查了平行线的性质和判定,切线的判定,相似三角形的性质和判定,垂径定理,勾股定理,扇形的面积,含30度角的直角三角形的性质的应用,能综合运用性质进行推理和计算是解此题的关键,有一定的难度.

练习册系列答案
相关题目
 如图,是一个正方体的展开图,正方体的每个面都有一个数字,只有一对相对两面的数字的积是有理数,这个有理数是( )
如图,是一个正方体的展开图,正方体的每个面都有一个数字,只有一对相对两面的数字的积是有理数,这个有理数是( )| A、4 | B、6 | C、9 | D、10 |
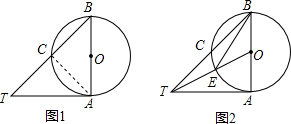 已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.
已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB. 如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,如果AC=
如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,如果AC=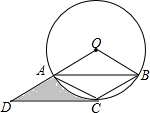 如图,⊙O是△ABC的外接圆,AC=BC,CD∥AB交OA的延长线于点D.
如图,⊙O是△ABC的外接圆,AC=BC,CD∥AB交OA的延长线于点D.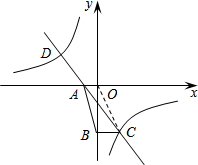 如图,直线y=kx+k(k≠0)与双曲线y=
如图,直线y=kx+k(k≠0)与双曲线y=