题目内容
已知在△ABC中,∠C=90°,AC=3,BC=4.在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,若旋转后点C的对应点C′和点A、点B正好在同一直线上,那么∠A′AC′的正切值等于 .
考点:旋转的性质
专题:计算题
分析:分类讨论:当C′点在线段AB上,如图1,连结AA′,先利用勾股定理计算出AB=5,在根据旋转的性质得BC′=BC=4,A′C′=AC=3,则AC′=AB-BC′=1,然后在Rt△AA′C′中,利用正切的定义即可得到tan∠A′AC′=
=3;当C′点在线段AB的延长线上,如图2连结AA′,根据旋转的性质得BC′=BC=4,A′C′=AC=3,则AC′=AB+BC′=9,然后在Rt△AA′C′中,根据正切的定义得到tan∠A′AC′=
=
.
| A′C′ |
| AC′ |
| A′C′ |
| AC′ |
| 1 |
| 3 |
解答:解:当C′点在线段AB上,如图1,连结AA′,
∵∠C=90°,AC=3,BC=4,
∴AB=
=5,
∵在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,
∴BC′=BC=4,A′C′=AC=3,
∴AC′=AB-BC′=1,
在Rt△AA′C′中,tan∠A′AC′=
=
=3;
当C′点在线段AB的延长线上,如图2, 连结AA′,
连结AA′,
∵在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,
∴BC′=BC=4,A′C′=AC=3,
∴AC′=AB+BC′=9,
在Rt△AA′C′中,tan∠A′AC′=
=
=
,
综合所述,∠A′AC′的正切值等于
或3.
故答案为
或3.
∵∠C=90°,AC=3,BC=4,

∴AB=
| AC2+BC2 |
∵在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,
∴BC′=BC=4,A′C′=AC=3,
∴AC′=AB-BC′=1,
在Rt△AA′C′中,tan∠A′AC′=
| A′C′ |
| AC′ |
| 3 |
| 1 |
当C′点在线段AB的延长线上,如图2,
 连结AA′,
连结AA′,∵在平面内将△ABC绕B点旋转,点A落到A′,点C落到C′,
∴BC′=BC=4,A′C′=AC=3,
∴AC′=AB+BC′=9,
在Rt△AA′C′中,tan∠A′AC′=
| A′C′ |
| AC′ |
| 3 |
| 9 |
| 1 |
| 3 |
综合所述,∠A′AC′的正切值等于
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了锐角三角函数的定义.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
在直角坐标平面中,M(2,0),圆M的半径为4,那么点P(-2,3)与圆M的位置关系是( )
| A、点P在圆内 | B、点P在圆上 |
| C、点P在圆外 | D、不能确定 |
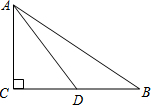 如图,在Rt△ABC中,∠C=90°,点D是BC边上的一点,CD=6,cos∠ADC=
如图,在Rt△ABC中,∠C=90°,点D是BC边上的一点,CD=6,cos∠ADC= 如图,抛物线y=-x2-4x+5交坐标轴于A、B、C三点,点P在第二象限的抛物线上,PF⊥x轴于F点,交AC于E点.若S△PAE:S△AEF=2:3,求P点坐标.
如图,抛物线y=-x2-4x+5交坐标轴于A、B、C三点,点P在第二象限的抛物线上,PF⊥x轴于F点,交AC于E点.若S△PAE:S△AEF=2:3,求P点坐标. 如图,图中有多少条线段,有多少条射线?并写出其中能用图中字母表示的线段.
如图,图中有多少条线段,有多少条射线?并写出其中能用图中字母表示的线段.
 如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD;
如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD;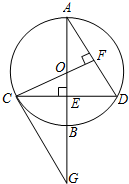 如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,
如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,