题目内容
 如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,如果AC=
如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,如果AC=| 5 |
考点:三角形的重心
专题:
分析:首先运用三角形重心的性质求出DG的长度,进而得到AD的长度;借助勾股定理即可解决问题.
解答: 解:∵点G是△ABC的重心,AG=2,
解:∵点G是△ABC的重心,AG=2,
∴DG=1,AD=3;
∵∠C=90°,
∴CD2=AD2-AC2,而AC=
,
∴CD=2,BC=2CD=4;
由勾股定理得:AB2=AC2+BC2,
∴AB=
.
故答案为
.
 解:∵点G是△ABC的重心,AG=2,
解:∵点G是△ABC的重心,AG=2,∴DG=1,AD=3;
∵∠C=90°,
∴CD2=AD2-AC2,而AC=
| 5 |
∴CD=2,BC=2CD=4;
由勾股定理得:AB2=AC2+BC2,
∴AB=
| 21 |
故答案为
| 21 |
点评:该题主要考查了三角形重心的性质及其应用问题;应牢固掌握三角形重心的性质,灵活运用该性质来分析、解答.

练习册系列答案
相关题目
下列四个图形中,不是正方体的展开图的是( )
A、 |
B、 |
C、 |
D、 |
用一个2倍放大镜照一个△ABC,下面说法中错误的是( )
| A、△ABC放大后,是原来的2倍 |
| B、△ABC放大后,各边长是原来的2倍 |
| C、△ABC放大后,周长是原来的2倍 |
| D、△ABC放大后,面积是原来的4倍 |
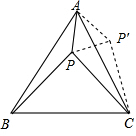 如图,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=
如图,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=
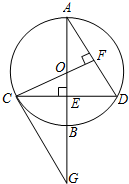 如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,
如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G, 阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布扇形统计图,其中八年级人数为408人,表是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题: