题目内容
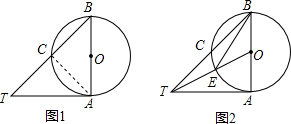 已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.
已知AB是⊙O的直径,AT与⊙O相切于点A,⊙O交BT于C,CT=CB.(1)如图1,求证:AB=AT;
(2)如图2,OT交⊙O于E,求tan∠TBE的值.
考点:切线的性质
专题:
分析:(1)欲证明AB=AT,只需证得AC是边BT上的中垂线;
(2)过B作BF∥AT交TO的延长线于F,过B作BG⊥TF于G,过E作EH⊥BT于H,设AB=2,则OA=OB=OE=1,AT=2,BT=2
,OT=
=
,根据△AOT∽△BOF,求得BF=AT=2,OF=OT=
,根据三角形的面积求得OF•BG=OB•BF,得出BG=
=
=
,OG=
=
,从而求得TG=OT+OG=
+
=
,根据△BTG∽△ETH,求得HE=
,HT=
,进而求得BH=2
-
=
,从而求得tan∠TBE的值.
(2)过B作BF∥AT交TO的延长线于F,过B作BG⊥TF于G,过E作EH⊥BT于H,设AB=2,则OA=OB=OE=1,AT=2,BT=2
| 2 |
| 22+12 |
| 5 |
| 5 |
| OB•BF |
| FO |
| 2 | ||
|
2
| ||
| 5 |
| OB2-BG2 |
| ||
| 5 |
| 5 |
| ||
| 5 |
6
| ||
| 5 |
5
| ||||
| 10 |
15
| ||||
| 10 |
| 2 |
15
| ||||
| 10 |
5
| ||||
| 10 |
解答: (1)证明:如图1,∵AB是⊙O的直径,
(1)证明:如图1,∵AB是⊙O的直径,
∴∠BCA=90°.
又∵CT=CB,
∴AC是边BT上的中垂线,
∴AT=AB.
(2)解:过B作BF∥AT交TO的延长线于F,过B作BG⊥TF于G,过E作EH⊥BT于H,
设AB=2,
∴OA=OB=OE=1,AT=2,BT=2
,OT=
=
,
∵△AOT∽△BOF,
∴
=
=
=1,
∴BF=AT=2,OF=OT=
,
∴OF•BG=OB•BF,
∴BG=
=
=
,
∴OG=
=
,
∴TG=OT+OG=
+
=
,
∵△BTG∽△ETH,
∴
=
=
,
∵TE=OT-OE=
-1,
∴
=
=
,
∴HE=
,HT=
,
∴∴tan∠TBE=
=
=
=
-2.
 (1)证明:如图1,∵AB是⊙O的直径,
(1)证明:如图1,∵AB是⊙O的直径,∴∠BCA=90°.
又∵CT=CB,
∴AC是边BT上的中垂线,
∴AT=AB.
(2)解:过B作BF∥AT交TO的延长线于F,过B作BG⊥TF于G,过E作EH⊥BT于H,
设AB=2,

∴OA=OB=OE=1,AT=2,BT=2
| 2 |
| 22+12 |
| 5 |
∵△AOT∽△BOF,
∴
| AT |
| BF |
| OT |
| OF |
| OA |
| OB |
∴BF=AT=2,OF=OT=
| 5 |
∴OF•BG=OB•BF,
∴BG=
| OB•BF |
| FO |
| 2 | ||
|
2
| ||
| 5 |
∴OG=
| OB2-BG2 |
| ||
| 5 |
∴TG=OT+OG=
| 5 |
| ||
| 5 |
6
| ||
| 5 |
∵△BTG∽△ETH,
∴
| HE |
| BG |
| ET |
| BT |
| HT |
| TG |
∵TE=OT-OE=
| 5 |
∴
| HE | ||||
|
| ||
2
|
| HT | ||||
|
∴HE=
5
| ||||
| 10 |
15
| ||||
| 10 |
∴∴tan∠TBE=
| HE |
| BH |
| ||||||
|
5
| ||||
5
|
| 5 |
点评:本题考查了切线的性质,圆周角的性质三角形相似的性质,勾股定理的应用以及解直角三角形,作出辅助线构建直角三角形是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
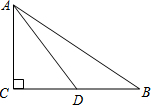 如图,在Rt△ABC中,∠C=90°,点D是BC边上的一点,CD=6,cos∠ADC=
如图,在Rt△ABC中,∠C=90°,点D是BC边上的一点,CD=6,cos∠ADC=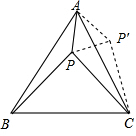 如图,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=
如图,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=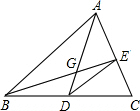 如图,已知AD是△ABC的中线,G是△ABC的重心,联结BG并延长交AC于点E,联结DE,则S△ABC:S△CED的值为
如图,已知AD是△ABC的中线,G是△ABC的重心,联结BG并延长交AC于点E,联结DE,则S△ABC:S△CED的值为 如图,抛物线y=-x2-4x+5交坐标轴于A、B、C三点,点P在第二象限的抛物线上,PF⊥x轴于F点,交AC于E点.若S△PAE:S△AEF=2:3,求P点坐标.
如图,抛物线y=-x2-4x+5交坐标轴于A、B、C三点,点P在第二象限的抛物线上,PF⊥x轴于F点,交AC于E点.若S△PAE:S△AEF=2:3,求P点坐标. 如图,图中有多少条线段,有多少条射线?并写出其中能用图中字母表示的线段.
如图,图中有多少条线段,有多少条射线?并写出其中能用图中字母表示的线段.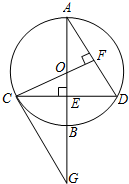 如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,
如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,